Некоторые конструкции целесообразных асимптотически-оптимальных симметрических автоматов

Рассмотрим некоторые конструкции автоматов и их поведение в стационарной случайной среде 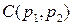. Стационарная случайная среда 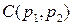означает, что за действие 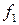среда с вероятностью 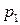получает вознаграждение, а с вероятностью 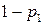штраф. За второе действие 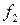среда выдает поощрение с вероятностью 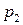, а с вероятностью 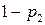- штраф.

1. Автоматы с линейной тактикой, предложенные М.Л. Цетлиным [3].

Рассмотрим простейший пример автомата, обладающего целесообразным поведением. Рассмотрим автомат 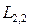, имеющий два состояния памяти 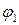и и 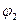два действия 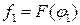и 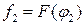. Автомат сохраняет свои состояния (действия) при выигрыше и изменяет при проигрыше. Матрицы состояний имеют вид 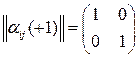, 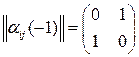. Графы переходов состояний имеют вид

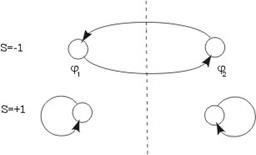
Рисунок 1

Найдем математическое ожидание выигрыша этого автомата в стационарной случайной среде С( 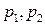). Обозначим через 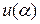( 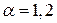) финальную вероятность действия 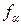. Тогда:

,

.

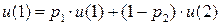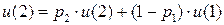Учитывая условие нормировки - 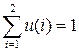, имеем:

,

.

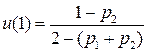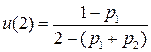Тогда математическое ожидание выигрыша 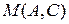автомата А в среде С определяется как:

.

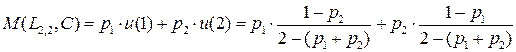
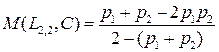Если автомат выбирает свои действия независимо от реакций среды и равновероятно, то математическое ожидание его выигрыша

.

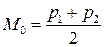Очевидно, что 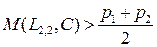при 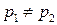, т.е. автомат 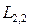обладает целесообразным поведением в стационарной случайной среде С ( ).

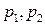Рассмотрим автомат 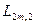(с линейной тактикой), являющийся естественным обобщением автомата 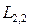. Он имеет 2m состояний 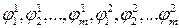и два различных действия 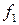и 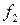. Графы переходов состояний имеют вид (рисунок 2):

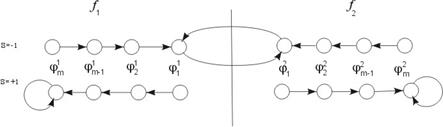
Рисунок 2

Рассмотрим поведение автомата 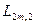в стационарной случайной среде 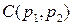. Пусть 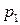> 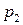. Докажем целесообразность его поведения, показав, что он выбирает с большей вероятностью то действие, у которого предпочтение больше: .

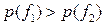Имеем дискретную цепь Маркова, задающую поведение системы “автомат – среда”. Как и раньше, 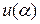( 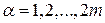) - финальная вероятность действия 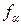. Зададим 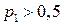; 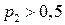. Найдем финальную вероятность 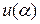каждого действия 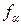, а затем математическое ожидание выигрыша.

……..

……….

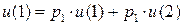
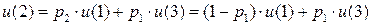
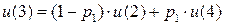
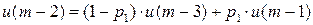
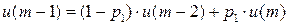
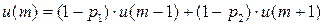
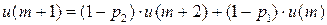
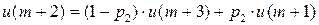
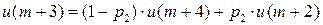
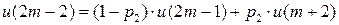
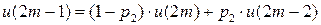
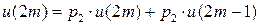
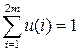- Условие нормировки

=

=

….

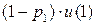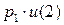
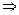
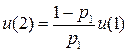
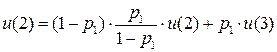
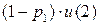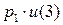
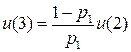
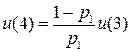
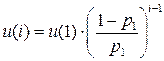
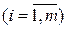
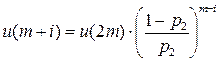
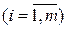
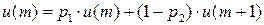
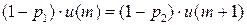
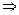
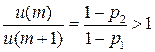, если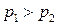

….

…

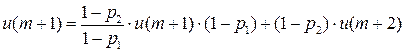
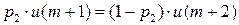
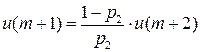
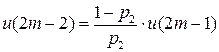
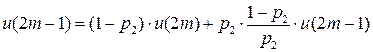
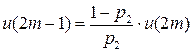
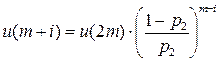
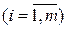
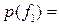
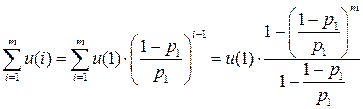
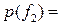
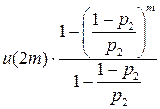
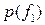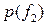> , если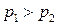

Мат. ожидание выигрыша возрастает, значит эти автоматы целесообразны.

Замечание: Если рассмотреть последовательность таких автоматов, у которых память 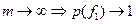, то такая последовательность автоматов называется асимптотически-оптимальной.

Автомат с линейной тактикой 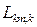является обобщением конструкций М.Л. Цетлина, рассмотренных выше. Автомат имеет 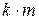внутренних состояний и 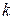действий (параметр 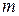- глубина памяти). Состоянием автомата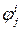 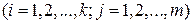соответствует выходное действие 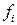. При 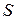= +1 (поощрении) автомат 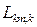не меняет своего действия 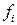и из состояния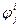 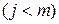переходит в состояние 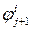, а в состоянии 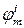остаётся. При 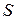= -1 (штрафе) из состояния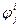 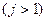переходит в состояние 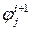при 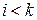и в состояние 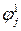при 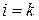, меняя своё действие 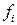на 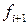( 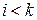) или на 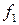( 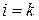). Граф смены состояний приведён на рисунке 3.

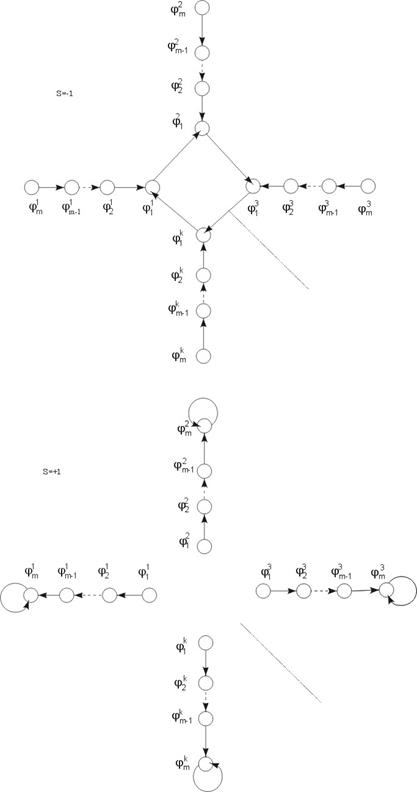
Рисунок 3

Автомат с линейной тактикой 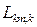также является целесообразным в стационарной случайной среде С( 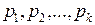), и относится к асимптотически-оптимальной последовательности автоматов.

2. Автомат Крылова .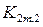

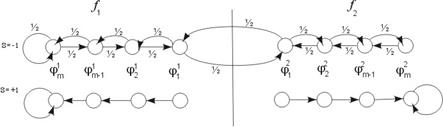
Рисунок 4

…

…

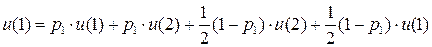
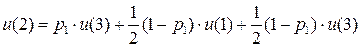
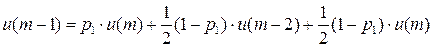
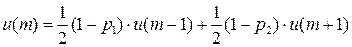
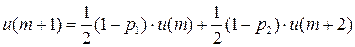
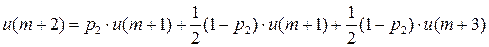
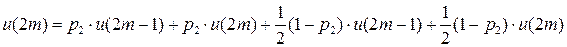
Добавляем условие нормировки: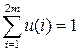

Тогда из первого уравнения 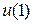получаем: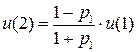

…

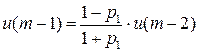
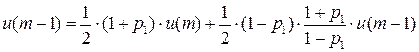
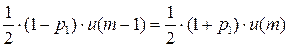
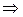
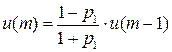
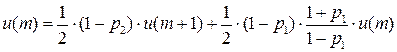
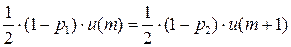
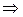
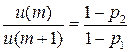
Итак, 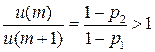, если 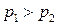. Т.е. математическое ожидание выигрыша возрастает, значит, эта конструкция обладает целесообразностью поведения.

Автоматы Крылова образуют асимптотически-оптимальную последовательность во всех стационарных случайных средах.

Аналогично, можно доказать целесообразность поведения автоматов, представленных ниже [2,3].

3. Автомат Роббинса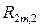

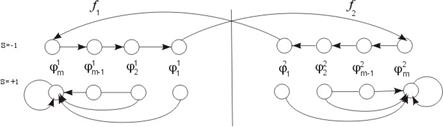
Рисунок 5

4. Автомат Кринского (“доверчивый” автомат)

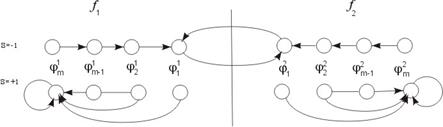
Рисунок 6

5. Автомат Вайсборда

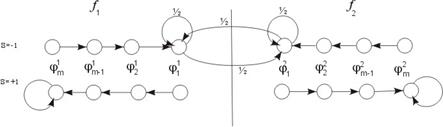
Рисунок 7

Запишем финальные вероятности состояний:

….

…

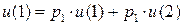
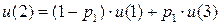
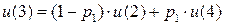
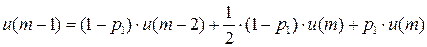
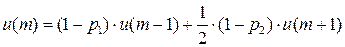
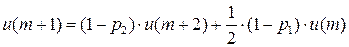
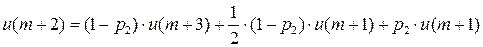
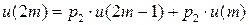
Автомат обладает целесообразностью поведения, т.к. 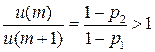, если .

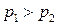6. Стохастический автомат с линейной тактикой 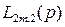. Данная конструкция представляет собой стохастический вариант автомата с линейной тактикой М.Л. Цетлина. При входном сигнале S автомат 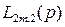с вероятностью 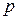осуществляет те же переходы, что и автомат 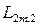при таком же входном сигнале, а с вероятностью 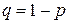автомат 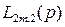осуществляет такие же переходы, которые осуществляет автомат 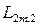при противоположном входном сигнале. При 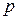=1 стохастический автомат 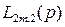становится детерминированным автоматом с линейной тактикой. Автомат 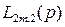при 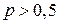является целесообразным в стационарной случайной среде С и относится к асимптотически-оптимальной последовательности автоматов.

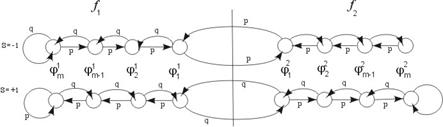
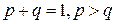
Рисунок 8

7. Автомат Валаха (с избирательной тактикой)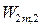

S = +1

S = ‑1

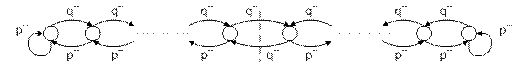
Рисунок 9

Граф смены состояний автомата Валаха аналогичен графу стохастического автомата с линейной тактикой, только при S = +1 вместо 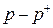, вместо 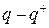: 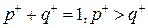, а в случае S = -1 вместо 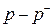, вместо :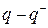