Критерий устойчивости Найквиста
Для наиболее часто встречающегося на практике случая, когда разомкнутая система устойчива, критерий Найквиста формулируется следующим образом. Если разомкнутая система автоматического управления устойчива, то замкнутая система автоматического управления будет устойчива, если амплитудно-фазовая характеристика разомкнутой системы W(jw) не охватывает точку (-1, j0).
Определение устойчивости астатических систем. При w = 0 частотная передаточная функция астатической системы обращается в ¥, а ее амплитудно-фазовая характеристика претерпевает разрыв. В этом случае поступают следующим образом. Для систем с астатизмом любого порядка n нужно построить амплитудно-фазовую характеристику разомкнутой системы в диапазоне частот 0 < w < ¥ и дополнить ее дугой окружности бесконечно большого радиуса, начинающейся на вещественной положительной полуоси и описывающей угол от 0 до - np/2 , и затем применить критерий устойчивости Найквиста.
С ростом коэффициента усиления разомкнутой системы модуль амплитудно-фазовой характеристики также растет, и при некотором значении коэффициента усиления K = Kгр, называемого граничным коэффициентом усиления, амплитудно-фазовая характеристика пройдет через точку
(- 1, j0), т.е. система будет на границе устойчивости. Если построена амплитудно-фазовая характеристика при некотором значении коэффициента усиления K, критический коэффициент усиления системы может быть вычислен следующим образом. Определяется модуль АФХ ½W(jw1)½ на частоте w1 , при которой фазовый сдвиг j(w1) = - p (величина отрезка, заключенного между 0 и точкой пересечения АФХ с отрицательной вещественной полуосью). Тогда
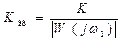 .
.
В данной лабораторной работе задаются два варианта структурных схем систем третьего порядка.

Рис. 5.1. Вариант А. Статическая система.
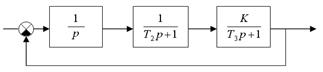
Рис. 5.2. Вариант Б. Астатическая система.
Вопросы к экзамену по дисциплине «Основы теории управления»
1. Введение. Виды систем автоматического управления.
2. Основные понятия и определения дисциплины.
3. Общие понятия о динамических звеньях.
4. Безынерционное звено.
5. Инерционное звено.
6. Интегрирующее звено.
7. Дифференцирующее звено.
8. Упругое звено.
9. Колебательное звено.
10. Параллельное соединение звеньев.
11. Последовательное соединение звеньев.
12. Замкнутые и разомкнутые САУ.
13. Структурные преобразования.
14. Временные характеристики динамических звеньев.
15. Частотные характеристики простых динамических звеньев.
16. Передаточная функция звена и системы.
17. Дифференциальные уравнения звеньев.
18. Устойчивость. Общее и необходимое условие устойчивости линейных систем.
19. Критерий устойчивости Гурвица.
20. Критерий устойчивости Найквиста.
21. Критерий устойчивости Михайлова.
22. Логарифмический критерий устойчивости.
23. Области и запасы устойчивости, способы их оценки.
24. Показатели качества переходных процессов.
25. Синтез линейных систем регулирования.
Рекомендуемая литература.
Основная литература.
1. Кочетков В.П. Основы теории управления. Ростов-на-Дону: Феникс,
2012. -412 с.
2. Мирошник И.В. Теория автоматического управления. Линейные системы: Учебное пособие для вузов. - СПб.: Питер, 2005. - 336 с.
3. Повзнер Л.Д. Теория систем управления: Учебное пособие для вузов. - М.: Изд. МГГУ, 2002. - 472 с.
4. Давыдов А.В. Основы теории управления. Тематические лекции: Учебное пособие в электронной форме. – Екатеринбург, УГГУ, ИГиГ, каф. ГИН. – http://www.prodav.narod.ru/otu/index.html.
5. Харитонов Ю.М., Зайцев О.Н. Теория автоматического управления. Чебоксары, 2007 г.
Дополнительная литература.
6. Семенов Е.М. и др. Автоматика и автоматизация производственных процессов: Методические указания по выполнению лабораторных и практических работ. – СПб ГЛТА, 2004. - 43 с.
7. Давыдов А.В. Лабораторные работы по курсу "Основы теории управления". Учебное пособие в электронной форме. – Екатеринбург, УГГУ, ИГиГ, ГИН. - http://www.prodav.narod.ru/otu/practical/otulab.doc.
