Основные теоретические положения. Методические указания к выполнению
ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ ЦЕПЕЙ
ПОСТОЯННОГО ТОКА
Методические указания к выполнению
расчетно-графической работы
Омск 2000
Составитель:
О.П. Куракина, канд. техн. наук, доц. каф. ТОЭ
В.Л. Федоров, канд. техн. наук, доц. каф. ТОЭ
1. ОБЩИЕ ЗАМЕЧАНИЯ ПО ОФОРМЛЕНИЮ И ВЫПОЛНЕНИЮ РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ
1. Расчеты выполняются на отдельных листах формата А4, а затем сшиваются.
2. Титульный лист пояснительной записки должен содержать следующие надписи: Омский государственный технический университет, кафедра «ТОЭ и ПЭ», полное наименование работы, номер варианта, фамилия студента и группа, фамилия преподавателя, Омск – 200…
3. Для каждой задачи должно быть полностью записано задание (содержание расчета), начерчена в соответствии с ГОСТ схема электрической цепи, приведены её параметры.
4. Пояснительную записку следует писать в настоящем времени, третьем лице, («определяем», «составляем» и т.п.), избегать сокращения слов.
5. Каждый этап расчета должен быть озаглавлен.
6. В записке нужно приводить не только расчетные формулы и конечные результаты, но также пояснения и необходимые промежуточные величины и вычисления, позволяющие понимать выполняемые действия и проверять их.
7. Везде у параметров, имеющих определенные размерности, писать в окончательных результатах соответствующие единицы измерения.
8. При записи результатов расчетов можно ограничиться четырьмя значащими цифрами, например: I = 0,08647 A; U = 16,09 B; P = 28160 Вт.
9. Все рисунки (схемы) должны быть пронумерованы. В тексте записки обязательно должны быть ссылки на соответствующие рисунки.
2. ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ ЭЛЕКТРИЧЕСКОЙ
ЦЕПИ ПОСТОЯННОГО ТОКА
Задачей расчета электрической цепи является определение токов в ее ветвях, потенциалов узлов, напряжений на отдельных участках (элементах) с последующей проверкой полученных результатов при помощи баланса мощностей. В процессе расчета часто применяют эквивалентные преобразования, которые заключаются в замене отдельных участков цепи более простыми. Замену осуществляют так, чтобы в остальной части цепи напряжения и токи не изменились. В результате эквивалентных преобразований упрощается исходная цепь и облегчается ее расчет.
Основные теоретические положения
Электрической схемой называется графическое изображение электрической цепи. Она показывает, как осуществляется соединение элементов цепи.
Ветвью называется участок цепи, образованный одним или несколькими последовательно включенными элементами, по которым течет один и тот же ток.
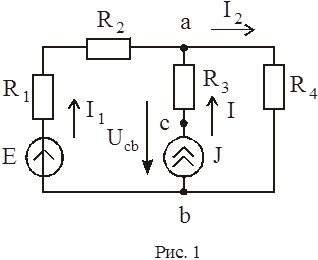Так, в схеме (рис.1) три ветви. Первая образована элементами Е, R 1, R 2; вторая – R 3, J; третья – одним сопротивлением R 4.
Узлом называется место соединения трех и более ветвей (точки “a” и “b” в схеме рис.1).
Пассивными называются ветви, не содержащие источников электрической энергии. Пример пассивного элемента – электрическое сопротивление R, в котором происходит преобразование электрической энергии
в тепловую.
Ветви, содержащие источники энергии, называются активными. Источниками электрической энергии являются генерирующие устройства, в которых энергия того или иного вида преобразуется в электрическую. В процессе расчета электрических цепей пользуются идеальными и реальными источниками ЭДС и тока.
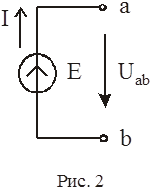
Идеальным источником ЭДС (рис. 2) называется активный элемент с двумя выводами, напряжение на зажимах которого не зависит от тока, протекающего через источник, т.е U ab = E.
Идеальный источник ЭДС является источником бесконечной мощности, его внутреннее сопротивление 
равно нулю. Стрелка внутри источника указывает на 
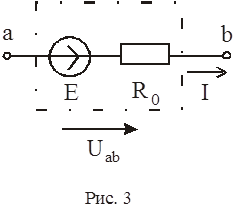
направление возрастания потенциала. . У реального источника ЭДС конечной мощности (рис. 3) внутреннее сопротивление R 0 не равно нулю. При увеличении тока, отдаваемого в нагрузку, происходит уменьшение напряжения U ab.
Идеальным источником тока (рис. 4) называется активный элемент с двумя выводами, ток которого не зависит от напряжения U ab на его зажимах. Идеальный источник является источником бесконечной мощности. Его внутренняя проводимость равна нулю, а внутреннее сопротивление – бесконечно велико. Схема замещения реального источника тока конечной мощности приведена на (рис. 5).
 |
. Закон Ома
Ток I и напряжение U на сопротивлении R связаны законом Ома следующим образом:
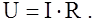(1)
Законы Кирхгофа
Электрические цепи постоянного тока могут быть рассчитаны с помощью законов Кирхгофа.
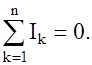
Первый закон Кирхгофа. . (2)
Алгебраическая сумма всех токов, сходящихся в любом узле, равна нулю. Токи, направленные к узлу, условно принимаются положительными, а направленные от него – отрицательными (или наоборот).
Второй закон Кирхгофа:
.
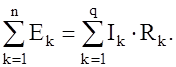. (3)
Алгебраическая сумма ЭДС замкнутого контура равна алгебраической сумме падений напряжений в нем. Направление обхода контура выбирается произволь-
но; при записи левой части равенства ЭДС, направления которых совпадают с выбранным направлением обхода, принимаются положительными, а ЭДС, направленные против выбранного обхода – отрицательными. При записи правой части равенства со знаком “+” берутся падения напряжения в тех ветвях, в которых положительное направление тока совпадает с направлением обхода, и со знаком “-“ – падения напряжения в тех ветвях, в которых положительное направление тока противоположно направлению обхода.
Если цепь содержит N в – ветвей, N у – узлов, N т – источников тока, то
1) устанавливается число неизвестных токов: N в – N т ;
2) число линейнонезависимых уравнений, составляемых по первому закону Кирхгофа, равно числу узлов без единицы: N у – 1 ;
3) число уравнений, составляемых по второму закону Кирхгофа:
К = N в – N y +1 – N т .
При составлении уравнений по второму закону Кирхгофа следует выбирать независимые контуры (каждый из которых содержит по сравнению с предыдущим хотя бы одну новую ветвь), не содержащие источников тока.
Так, для цепи (рис. 1) система уравнений имеет вид
 |
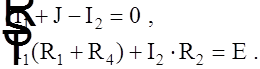Баланс мощностей
Пусть в электрической цепи имеются источники и приемники электрической энергии. Тогда условие баланса мощностей, являясь следствием закона сохранения энергии, формулируется следующим образом: суммарная мощность, генерируемая источниками энергии, равна суммарной мощности, потребляемой в цепи:
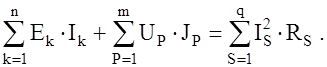
(4)
Здесь n – число ветвей, содержащих источники ЭДС;
m – число ветвей, содержащих источники тока;
UP – напряжение на зажимах источника тока;
q – число ветвей, содержащих сопротивления.
Мощность источника может быть положительной (если направление тока совпадает с направлением ЭДС Е k или напряжения UP) или отрицательной (направления тока и ЭДС противоположны или UP отрицательно). Отрицательный знак мощности означает, что соответствующий источник работает в режиме потребления энергии.
 |
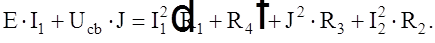Так, для цепи (рис.1) баланс мощностей имеет вид