Общая схема алгоритма с возвратом
Пусть решение, которое мы ищем, имеет вид последовательности <X(1), …, X(n)>.
Будем строить его, начиная с пустой последовательности длины 0.
Пусть на каком-то этапе уже построено частичное (неполное) решение длины i: < X(1), …, X(i) >.
Попытаемся продолжить это решение еще на один шаг. Для этого нужно отыскать допустимое X(i+1). X(i+1) считается допустимым, если или < X(1), …, X(i+1) > уже является решением, или относительно < X(1), …, X(i+1) > нельзя сразу сказать, что его невозможно расширить до полного решения.
Дальше существует две возможности:
– если X(i+1) допустимо, то следующее допустимое X ищется для частичного решения <X(1), …, X(i+1)> (заметим, что допустимость X(i+1) вовсе не означает, что <X(1), …, X(i+1)> можно расширить до полного решения);
– если допустимого X(i+1) не существует, то возвращаемся на шаг назад – к частичному решению < X(1), …, X(i-1) > и для него отыскиваем другое X’[i], не совпадающее с предыдущим X(i).
Более точно, пусть для каждого i>0 существует множество A(i), из которого будут выбираться X(i) – претенденты на i–ю координату частичного решения.
Очевидно, множества A(i) должны содержать все X(i), занимающие i-ю координату любого решения. Кроме того, A(i) всегда будут содержать какие-то лишние элементы, не содержащие в i–й координате ни одного решения.
Теперь общая схема алгоритма с возвратом имеет следующий вид:
1 begin
2 k:= 1;
3 while k>0 do
4 if существует еще новый y Î A(k),
являющийся допустимым then
5 begin
6 X[k]:= y; {y использован}
7 if <X[1],…,X[k]> является решением then
write (<X[1],…,X[k]>);
8 k:= k+1
9 end
10 else {возврат на предыдущее частичное решение,
все элементы A(k) становятся
неиспользоваными}
11 k:= k-1
12 end.
Если предположить, что все решения имеют длину, меньшую n+1, и все множества A(k) состоят из конечного числа элементов, то этот алгоритм находит все решения.
Тот же самый алгоритм можно очень просто записать с помощью рекурсии.
{рекурсивный вариант алгоритма с возвратом}
1 procedure BC(k);
{генерируем все решения, являющиеся продолжением
частичного решения <X[1],…,X[k-1]>, массив Х–
глобальный}
2 begin
3 for y Î A(k) do
4 if y допустим then
5 begin
6 X[k]:= y;
7 if <X[1],…,X[k]> – решение then
8 write(<X[1],…,X[k]>);
9 BC(k+1);
{генерируем все решения, являющиеся продолжением частичного решения <X[1],…,X[k-1],y>}
10 y неиспользован;{возврат на <X[1],…,X[k-1]>}
11 end {цикл 3 выберет для продолжения
<X[1],…,X[k-1]> следующий y'¹y}
12 end;
Вопрос 1. Каким образом частичное решение <X(1), …, X(k)> будет продолжено внутри BC(k+1)?
Сгенерировать все решения можно вызовом ВС(1) из главной программы. Описание алгоритма возврата мы начали с несколько более сложного нерекурсивного варианта, так как в рекурсивном варианте «возврат» является частью механизма рекурсии и не появляется в явном виде.
ЗАДАЧА ГАМИЛЬТОНА
Применим теперь алгоритм с возвратом для поиска всех гамильтоновых циклов в графе G=<V,E>. Каждый такой цикл – последовательность различных вершин графа <X(1), …, X(n+1)> и только X(1) = X(n+1) = k, где k – произвольная фиксированная вершина, соседние вершины X(i) и X(i+1) соединены ребром.
Тогда A(i) = V (множество всех вершин) для любого i £ n+1;
Условие допустимостиy для продолжения <X(1), …, X(i-1)>:
1. y Î ЗАПИСЬ[X(i-1)] (вершина y соединена ребром с X(i-1));
2. y новая, то есть не принадлежит <X(1), …, X(i-1)>.
АЛГОРИТМ {Нахождение всех гамильтоновых циклов в графе}
Данные: Граф G=<V,E>, представленный списками ЗАПИСЬ[v], v Î V.
Результаты: Печать всех гамильтоновых циклов графа G.
Переменные ЗАПИСЬ, X, DOP – глобальные.
1 procedure GAMI(i);
{генерация всех гамильтовых циклов, являющихся
продолжением частичного решения <X[1],…,X[i-1]>}
2 begin
3 for y Є ЗАПИСЬ[X[i-1]] do
4 if (i=n+1) AND (y=k) then
5 write(X[1],…,X[n],k)
6 else if DOP[y] then
7 begin
8 X[i]:= y; DOP[y]:= ложь;
9 GAMI(i+1);
10 DOP[y]:= истина;
{все решения, продолжающие <X[1],…,X[i-1],y> уже сгенерированы, выбираем другое y', а y становится неиспользованным}
10 end
11 end;{GAMI}
1 begin {основная программа}
2 for v Є V do DOP[V]:= истина;
3 X[1]:= k ; {k – произвольная}
4 DOP[k]:= ложь;
5 GAMI(2);
6 end.
Протрассируем алгоритм для модельного графа и построим его дерево поиска (рис. 9.2):
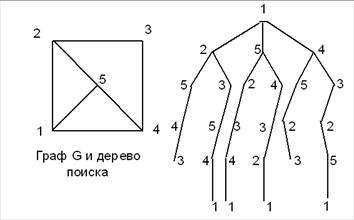
Рис. 9.2. Трассировка алгоритма
Сложность этого алгоритма в наихудшем случае растет по экспоненте с ростом n.
Это справедливо и для случая, когда ищется ровно одно решение (если задача не имеет решения, то эта модификация не влияет на ход выполнения алгоритма).
Вопрос 2. Докажите, представив соответствующий «плохой» граф, что число шагов в алгоритме нахождения всех гамильтоновых циклов растет экспоненциально с ростом n.
Ответ 1. Во всех направлениях, до всех тупиков и полных решений.
Ответ 2. Граф типа «погремушка». Такой граф не содержит ни одного гамильтонова цикла, в то же время все вершины, кроме V0, соединены и представляют собой клику, т.е. граф, у которого все вершины соединены попарно. Всего различных путей будет n!, а для проверки каждой uj из них потребуется n шагов, итого n*n!, что растет быстрее экспоненты (рис. 9.3).
| |
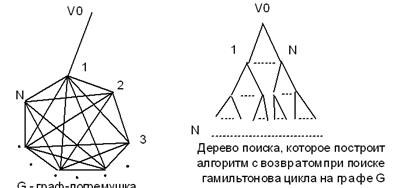
Рис. 9.3. Граф «погремушка»
