Классическая вероятность

Задача. Определить вероятность ничьей в турнире из 4-х встреч двух равносильных игроков (команд), если ничьи в отдельной встрече не допускаются (пенальти, дополнительное время и т.п.).

Поскольку противники равносильные, количество встреч четно и каждая из них может закончиться только победой или поражением, то внутренний голос достаточно уверенно нашептывает про ½ или 50%. Чтобы доказать правильность этого интуитивного ответа или опровергнуть его перечислим все мыслимые исходы матча и отберем среди них благоприятные. Заметим, что достаточно рассматривать итоги встреч с позиции только одного игрока, т.к. его победа означает поражение противника и наоборот. Возьмем одного игрока, условно называемого первым, и опишем его победу цифрой “1”, а поражение - ”0”. Знаки в кавычках могут рассматриваться как числа или символы. Теперь можно составить таблицу с перечислением всех мыслимых исходов турнира. Первая строка первого столбца таблицы отвечает наиболее желаемому исходу турнира первого игрока - его победе во всех 4-х встречах. Далее в первом столбце идут игры с одним поражением в первой, второй и т. д. встречах. Второй столбец описывает игры с ничьей по итогам всех 4-х встреч. В трех первых строках последнего столбца обозначена только одна победа и в его последней строке стоит сокрушительный сухой разгром первого игрока. Всего в таблице 16 равновозможных и несовместных исходов, среди которых 6 благоприятных для ничьей по итогам турнира (средний столбец). Теперь, следуя правилу вычисления классической вероятности, найдем вероятность ничьей Р(“ничья”)= , т.е. свести вничью турнир с четным числом встреч двум равносильным противникам менее вероятно нежели выиграть или проиграть. 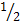Полученный результат изначально вовсе не очевиден и свидетельствует, что интуиция нас изрядно подвела, поскольку относительная ошибка составила ( - )/ = = 33,3%.

1 1 1 1	0 0 1 1	0 0 0 1
0 1 1 1	0 1 0 1	0 0 1 0
1 0 1 1	0 1 1 0	0 1 0 0
1 1 0 1	1 0 0 1	1 0 0 0
1 1 1 0	1 0 1 0	0 0 0 0
	1 1 0 0

При наличии такой таблицы нетрудно рассчитать вероятности других возможных результатов матча. Например:

Р(“выиграть”)= =Р(“проиграть”),

Р(“не проиграть”)= =Р(“не выиграть”),

Р(“выиграть всухую”)= = Р(“проиграть всухую”),

Р(“выиграть хотя бы один раз”)= =Р(“проиграть хотя бы один раз”).

Здесь наблюдается своеобразная симметрия рассмотренных событий. Уместно отметить также, что противоположным к “выиграть” является не “проиграть”, а “не выиграть”. Сумма именно этих исходов является достоверным событием, а сумма их вероятностей равна 1.

Задача. Найти вероятность выпадения двух орлов и хотя бы одного орла в двух бросаниях монеты. Поскольку орел ”О” и решка ”Р” события равновозможные Р(О)=Р(Р)=0.5, то применима схема классической вероятности, в соответствии с которой

Р(ОО)=Р(О)Р(О)= , Р(О+О)=Р( )=1-Р(РР)=1- = .

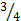Тот же результат даст таблица возможных исходов, которая применима в силу равновозможности выпадения орла и решки.

Условная вероятность

Задача. Какова вероятность из урны с 6 белыми и 3 черными шарами извлечь первым черный, а вторым белый шар.

В соответствии со схемой условной вероятности расчет производится по формуле

Р(А)=Р(БЧ)=Р(Б|Ч)Р(Ч)= · = =25 %.

Задача. При усложнении предыдущей задачи условием достать третьим черный шар искомой оказывается вероятность произведения событий ЧБЧ, которое мы препарируем следующим образом

Р(ЧБЧ)=Р(Ч|БЧ)Р(БЧ)=Р(Ч|БЧ)Р(Б |Ч)Р(Ч)= · · = · = ≈7 %.