Выбор корректирующих звеньев. Метод желаемых ЛЧХ

Метод логарифмических частотных характеристик используется для определения частотных передаточных функций корректирующих устройств, приближающих динамические показатели к желаемым. Наиболее эффективно этот метод применяется для синтеза систем с линейными или цифровыми корректирующими устройствами, поскольку в таких системах частотные характеристики звеньев не зависят от амплитуды входных сигналов.

Исходную систему обычно рассматривают как систему, состоящую из корректирующего звена, звена привода и звена объекта (рисунок 2.6)..

Рисунок 2.6 – СУ состоящая из корректирующего звена, звена привода и звена объекта

Синтез СУ методом логарифмических частотных характеристик включает в себя следующие операции.

На первом этапе по известной передаточной функции неизменяемой части СУ:

,

строится ее логарифмическая частотная характеристика

В большинстве случаев достаточно использование асимптотических частотных характеристик.

На втором этапе строится желаемая логарифмическая частотная характеристика СУ, которая удовлетворяла бы поставленным требованиям. Определение вида желаемой ЛАЧХ проводится исходя из назначения системы, времени переходного процесса, перерегулирования и коэффициентов ошибок. При этом часто используются типовые частотные характеристики для систем с разным порядком астатизма. При построении желаемой ЛАЧХ необходимо быть уверенным, что вид амплитудной характеристики полностью определяет характер переходных процессов, и нет необходимости вводить в рассмотрение фазовую частотную характеристику. Последнее справедливо в случае минимально-фазовых систем, для которых характерно отсутствие нулей и полюсов, расположенных в правой полуплоскости. При выборе желаемых логарифмических амплитудной и фазовой характеристик важно, чтобы последняя обеспечила требуемый запас устойчивости при частоте среза системы.

На последнем этапе из сравнения частотных характеристик некорректированной системы и желаемых частотных характеристик определяются частотные свойства корректирующего устройства. При использовании линейных средств коррекции логарифмическая частотная характеристика последовательного корректирующего устройства (ПКУ) может быть найдена вычитанием ЛАЧХ некорректированной системы из желаемой ЛАЧХ СУ, то есть:

.

Пример-2.Применительно к рисунку 2, передаточные функции объекта и привода имеют вид:

.

Методом логарифмических частотных характеристик определить передаточную функцию корректирующего устройства с учетом требований к системе:

1) У системы при отработке сигналов, меняющихся со скоростью - , ошибка .

2) Требуемое время регулирования .

3) Ошибка воспроизведения гармонических сигналов при должна быть не более , где - гармонический сигнал.

Решение: Находим передаточную функцию неизменяемой части СУ:

.

Система обладает астатизмом первого порядка, поэтому низкочастотная часть ЛЧХ должна иметь наклон –20дБ/дек.

Вычисляем коэффициент передачи системы на частоте .

Определяем сопрягающие частоты: .

Строим ЛЧХ , рисунок 2.7.

Построение желаемой ЛЧХ

Чтобы обеспечить удовлетворительное качество переходных процессов, наклон ЛАЧХ в диапазоне должен быть –20дБ/дек, и протяженность этого интервала должна быть не меньше 1декады. Исходя из требований к длительности переходного процесса, определяем частоту среза желаемой ЛАХ :

, , .

Учитывая требования по точности, находим точку . Эта точка является контрольной для построения низкочастотного участка ЛАХ :

.

Требования по воспроизведению гармонических сигналов: . График ЛАХ представлен на рисунке 2.7.

Рисунок 2.7 – Графики ЛЧХ

Построение ЛЧХ КУ

Логарифмическую частотную характеристику корректирующего устройства находим вычитанием ЛЧХ некорректированной системы из желаемой ЛЧХ. По ЛЧХ определяем передаточную функцию и параметры КУ:

. (2.11)

Последним этапом синтеза устройства коррекции является проверочный расчет СУ, который заключается в построении графиков переходных процессов для системы с выбранным корректирующим устройством. На этом этапе целесообразно использование средств вычислительной техники и моделирующих программных комплексов WorkBench, MathCAD и др.

На рисунке 2.8 представлены структурная схема неизменяемой части СУ и график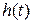и и при воздействиях вида и соответственно. На рисунке 2.9 показана схема СУ с корректирующим устройством, передаточная функция , которого определена выражением (2.11), а также график ошибки и переходного процесса при воздействии вида и соответственно.

Рисунок 2.8 – Структурная схема и переходные процессы

нескорректированной СУ

Рисунок 2.9– Переходные процессы скорректированной СУ

Анализ графиков рисунка 2.9 позволяет сделать вывод о том, что требования к системе по точности и длительности переходного процесса выполнены.

В ПК МВТУ полученную можно представить одним блоком, реализующим математическую модель звена общего вида.