Методические указания для выполнения

Контрольной работы

Пример 8.1.Вычислить предел функции .

Решение. В данном примере имеем неопределенность вида .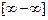

Преобразуем выражение:

В результате преобразований получили неопределенность вида 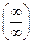. Для вычисления предела разделим оба многочлена на x в старшей степени, то есть на , получим

Здесь учитывается, что .

Ответ: .

Пример 8.2.Вычислить предел функции .

Решение.Подставляя 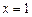получим неопределенность:

.

Разложим числитель и знаменатель на множители. Для этого найдем корни квадратных уравнений:

.

.

Получим:

.

Сократим на общий множитель 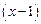и получим

.

Ответ:

При решении примера 2 можно было воспользоваться правилом Лопиталя:

Пример 8.3.Вычислить предел функции .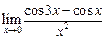

Решение.Подставляя 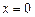получим неопределенность:

.

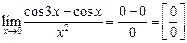Используя тригонометрическую формулу, преобразуем числитель в произведение:

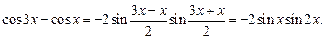
В результате получаем

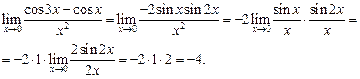
Здесь учитывается второй замечательный предел .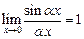

При решении примера 8.3 можно было дважды воспользоваться правилом Лопиталя:

Пример 8.4.Вычислить производную функции

.

Решение.Преобразуем иррациональные и дробные выражения, используя формулы

:

.

Воспользуемся правилами нахождения производной и таблицей производных, получим:

Ответ:

Пример 8.5.Вычислить производную функции .

Решение.Воспользуемся правилом нахождения производной от произведения двух функций

.

Производная функции 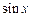определяется по таблице производных, а для определения производной функции воспользуемся правилом нахождения производной от сложной функции.

.

В итоге получим

.

Ответ: .

Пример 8.6.Вычислить производную функции .

Решение.

Воспользуемся правилом нахождения производной от частного двух функций и таблицей производных

Ответ:

Пример 8.7.Вычислить производную функции .

Решение.

Воспользуемся правилом нахождения производной сложной функции и таблицей производных.

Обозначим , , тогда получим .

Ответ:

Пример 8.8.Исследовать функцию и построить график

.

Решение.

1) Функция определена при всех значениях 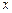кроме 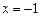, то есть в интервалах .

2) График функции пересекает ось Ох в точках, в ко­торых , так как дискриминант данного квадратного уравнения , то точек пересечения с осью Оx у данной функции нет.

С осью Оу функция пересекается при 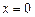, тогда . Таким образом точка (0;2) – точка пересечения с осью Оу.

3) Вертикальной асимп­тотой является прямая 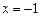, так как

, .

Найдем наклонную асимптоту :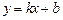

Таким образом, - наклонная асимптота.

4) Проверим четность, нечетность функции:

.

Так как , то функция не является ни четной, ни нечетной, поэтому у графика нет симметрии ни относительно оси ординат, ни относительно начала координат.

5) Найдем интервалы возрастания, убывания и точки экстремума функции.

Для нахождения точек возможного экстремума вычислим первую производную:

Найдем критические точки, прировняв производную к нулю:

.

Критические точк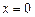и и 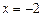. Эти точки разбивают область определения функции на четыре интервала: .

Определим знаки производной на этих интервалах:

, ,

, .

Рассмотрим результаты исследования в таблице.

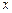		-2		(-1;0)
	+		-	-		+
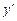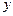	возрастает	-2	убывает	убывает	min	возрастает

6) Найдем интервалы выпуклости и точки перегиба функции.

Для определения критических точек вычислим вторую производную:

Итак, не обращается в нуль ни в одной точке, следовательно, точек перегиба нет.

Определим знаки второй производной в области определения функции:

,

Построим таблицу:

	-	+

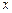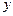7) На основании полученных данных строим график функции (рисунок 8.1).

Рисунок 8.1 - График функции

Пример 8.9.На 2 товара по ценам и 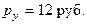Сергей тратит в месяц 120 руб. Определить оптимальный выбор, если его функция полезности .

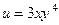Решение.Найдем максимум функции 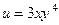при условии 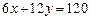. Выразим из условия переменную x и подставим ее в функцию полезности: , .

В результате получили функцию одной переменной. Найдем ее производную и приравняем ее к нулю.

.

Критические точки и . Эти точки разбивают область определения функции на три интервала: .

Определим знаки производной на этих интервалах:

	-	+	-

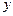Получили, что - точка максимума, . Таким образом, оптимальный выбор товаров составит 4 ед. и 8 ед.

9 Контрольные вопросы для зачета

Что нужно знать:

1.Определение функции. Область определения функции.

2.Способы задания функции.

3. Классификация функций.

4. Определение последовательности. Предел последовательности.

5.Определение предела функции.

6.Понятие бесконечно малых величин. Их свойства.

7. Понятие бесконечно больших величин. Их свойства.

8. Основные теоремы о пределах.

9. Первый и второй замечательные пределы.

10. Понятие односторонних пределов

11. Определение непрерывности функции.

12. Свойства непрерывных функций.

13. Определение точек разрыва 1 и 2 рода.

14. Определение производной функции.

15. Геометрический и физический смысл производной.

16. Понятие дифференциала.

17. Геометрический смысл дифференциала.

18. Основные правила дифференцирования.

19. Свойства дифференциала.

20. Дифференцируемость и непрерывность функции.

21. Производная сложной и обратной функции.

22. Производные высших порядков.

23. Дифференциалы высших порядков.

24. Правило Лопиталя.

25. Теорема Ферма.

26. Теорема Ролля.

27. Теорема Лагранжа.

28. Определение экстремумов функции.

29. Необходимый признак существования экстремума.

30. Достаточные признаки существования экстремума.

31. Условия постоянства, возрастания и убывания функции.

32. Признак выпуклости и вогнутости графика функции.

33. Признак точки перегиба.

34. Понятие асимптоты.

35. Способ нахождения вертикальной асимптоты.

36. Способ нахождения горизонтальной асимптоты.

37. Способ нахождения наклонной асимптоты.

38. Общая схема исследования функции.

39. Понятие функции нескольких переменных.

40. Частное приращение функции.

41. Полное приращение функции.

42. Понятие частной производной первого порядка.

43. Понятие частных производных второго порядка.

44. Полный дифференциал функции.

45. Понятие градиента функции.

46. Понятие экстремума функции двух переменных.

47. Необходимые условия экстремума.

48. Достаточные условия экстремума.

49. Понятие условного экстремума.

50. Методы нахождения условного экстремума.

Что нужно уметь:

1. Находить область определения функции.

2. Находить предел функции.

3. Раскрывать неопределенности вида .

4. Раскрывать неопределенность вида .

5. Исследовать функцию на непрерывность.

6. Находить производную функции с помощью основных правил дифференцирования.

7. Находить производную сложной функции.

8. Находить предел функции по правилу Лопиталя.

9. Находить экстремум функции.

10. Находить точки перегиба функции.

11. Находить асимптоты функции.

12. Находить частные производные.

13. Находить экстремум функции двух переменных.

14. Находить условный экстремум функции.