Криптосистема Гольдвассер-Микали

Параметры системы: n=pq – число Блюма, z – случайное число из .

Открытый ключ для шифрования – пара (n,z), секретный ключ для расшифрования – пара (p,q).

Пусть x₁, x₂, … , x_m – последовательность бит открытого текста. Бит шифрованного текста вычисляем по биту открытого текста как , где a_i – случайное число из Z_n.

В итоге шифрования получается последовательность не бит, а чисел, причем y_i является псевдоквадратом по модулю n, если x_i =1, и квадратом, если x_i=0.

Адресату, обладающему секретным ключом, отправляется последовательность чисел шифртекста y₁, y₂, …, y_m , после чего параметр z может быть уничтожен.

Адресат осуществляет расшифрование следующим образом:

, i=1,2,…,m.

Условная стойкость криптосистемы Гольдвассер-Микали основана на предположительной сложности алгоритма распознавания квадратов и псевдоквадратов по модулю Блюма без знания разложения модуля на простые сомножители.

Данная криптосистема имеет существенный недостаток – размер шифртекста значительно превышает размер открытого текста, ведь каждый бит последнего при шифровании преобразуется в число такой же размерности, как n.

Первообразные корни и индексы. Порождающий элемент и дискретный логарифм.

В этом параграфе рассмотрены теоретико-числовые основы, ведущие к задачам дискретного логарифмирования над конечным полем, а также приведены некоторые приложения теории конечных групп к таким вопросам как тесты на простоту и построение простых чисел.

Основные понятия и теоремы.

При (a,m)=1 существуют положительные γ с условием a^γ≡1(mod m). Наименьшее из таких γ называется показатель, которому a принадлежит по модулю m.

В том, что такие γ существуют, можно убедиться, вспомнив теорему Эйлера (γ=φ(m)).

Возвращаясь к основам общей алгебры, в частности, к теории конечных групп, можно сказать, что показатель, которому которому a принадлежит по модулю m есть то же самое, что порядок элемента a в конечной мультипликативной группе <U_m, · mod m>. Далее будем обозначать его O_m(a).

Поскольку дальнейшие построения будут тесно связаны с группой <U_m, · mod m>, то на протяжении текущего параграфа для краткости будем обозначать эту группу как U_m.

Докажем несколько важных теорем, описывающих свойства O_m(a):

Теорема 1.

Числа 1=a⁰, a¹, a², … , несравнимы между собой по модулю m.

Доказательство:

Действительно, из того, что a^l≡a^k(mod m), 0 ≤ k < l < O_m(a) следовало бы, что a^l—k≡1(mod m), 0 < k—l < O_m(a), что противоречит определению O_m(a).

□

Теорема 2.

Пусть δ= O_m(a). Тогда a^γ≡a^β (mod m) 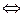γ≡β(mod δ).

Доказательство:

Из теоремы 1 следует, что если a^γ≡a^β (mod m) , то γ≡β(mod δ).

Пусть теперь γ≡β(mod δ) Тогда, по теореме делимости, найдутся такие числа q, w, r: 0 ≤ r <δ, что γ=δ·q+r, β=δ·w+r. Тогда из того, что a^δ≡1(mod m) следует, что

a^γ≡a^δq+r≡(a^q)^δa^r≡a^r(mod m)

a^β≡a^δw+r≡(a^w)^δa^r≡a^r(mod m)

Что и требовалось доказать.

□

Теорема 3.

O_m(a)\φ(m).

Доказательство:

Следует из Теоремы 2 при β=0 и из теоремы Эйлера (a^φ(m)≡1(mod m)).

□

Последняя теорема также может быть доказана как следствие из теоремы Лагранжа (порядок любого элемента в группе делит порядок группы) применительно к группе U_m.

Числа, принадлежащие показателю φ(m) (если они существуют), называются первообразными корнями по модулю m.

Если a – первообразный корень по модулю m, то согласно Теореме 1, числа 1=a⁰, a¹, a², … , a^φ(m)-1 несравнимы между собой по модулю m, а раз их φ(m) штук, то они образуют приведенную систему вычетов по модулю m. Тогда a есть ни что иное как порождающий элемент группы U_m.

Утверждение

Если существует первообразный корень по модулю m, то мультипликативная группа U_m является циклической группой.

Доказательство очевидным образом следует из вышесказанного.

Пример 1.

Рассмотрим группу U₁₁=<{1,2,3,4,5,6,7,8,9,10},· mod m>. Порядок этой группы равен φ(11)=10. Найдем порядки всех элементов в этой группе и отыщем порождающий элемент этой группы, если он существует. Для краткости вместо a^b mod 11 будем писать просто a^b.

1: 1⁰=1, 1¹=1. O₁₁(1)=1.

2: 2⁰=1, 2¹=2, 2²=4, 2³=8, 2⁴=5, 2⁵=10, 2⁶=9, 2⁷=7, 2⁸=3, 2⁹=6, 2¹⁰=1. O₁₁(2)=10.

3: 3⁰=1, 3¹=3, 3²=9, 3³=5, 3⁴=4, 3⁵=1. O₁₁(3)=5.

4: 4⁰=1, 4¹=4, 4²=5, 4³=9, 4⁴=3, 4⁵=1. O₁₁(4)=5.

5: 5⁰=1, 5¹=5, 5²=3, 5³=4, 5⁴=9, 5⁵=1. O₁₁(5)=5.

6: 6⁰=1, 6¹=6, 6²=3, 6³=7, 6⁴=9, 6⁵=10, 6⁶=5, 6⁷=8, 6⁸=4, 6⁹=2, 6¹⁰=1. O₁₁(6)=10.

7: 7⁰=1, 7¹=7, 7²=5, 7³=2, 7⁴=3, 7⁵=10, 7⁶=4, 7⁷=6, 7⁸=9, 7⁹=8, 7¹⁰=1. O₁₁(7)=10.

8: 8⁰=1, 8¹=8, 8²=9, 8³=6, 8⁴=4, 8⁵=10, 8⁶=3, 8⁷=2, 8⁸=5, 8⁹=7, 8¹⁰=1. O₁₁(8)=10.

9: 9⁰=1, 9¹=9, 9²=4, 9³=3, 9⁴=5, 9⁵=1. O₁₁(9)=5.

10: 10⁰=1, 10¹=10, 10²=1. O₁₁(10)=2.

Действительно, порядки всех элементов делят порядок группы. При этом в группе U₁₁ нашлись порождающие элементы, причем не один, а четыре. Это 2, 6, 7 и 8. Однако не во всех группах U_m существуют порождающие элементы, убедимся в этом на следующем примере:

Пример 2.

Рассмотрим группу U₈=<{1,3,5,7},· mod 8>, φ(8)=4.

1: 1⁰=1, 1¹=1. O₈(1)=1.

3: 3⁰=1, 3¹=3, 3²=1. O₈(3)=2.

5: 5⁰=1, 5¹=5, 5²=1. O₈(5)=2.

7: 7⁰=1, 7¹=7, 7²=1. O₈(7)=2.

Итак, в группе U₈ нет порождающего элемента.

Возникает вопрос – в каких группах U_m порождающий элемент существует, а в каких – нет, и как найти порождающий элемент? На этот вопрос ответим в следующих пунктах данного параграфа.

6.2. Существование первообразных корней по модулю p.

Лемма 1.

O_m(x)=ab 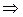O_m(x^a)=b.

Лемма 2.

O_m(x)=a, O_m(y)=b, (a,b)=1 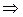O_m(xy)=ab.

Доказательства этих лемм не представляют принципиальной сложности, поэтому предоставляются читателю в качестве упражнения.