Геометрический вектор, линейные операции над векторами
Метод Крамера решения СЛАУ
Рассмотрим СЛАУ, в которой число уравнений совпадает с числом неизвестных
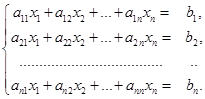 (1)
(1)
Введем обозначения 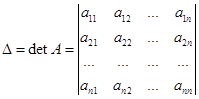 ,
, 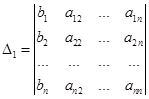 ,
, 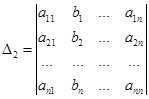 , …,
, …, 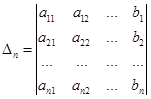 . Здесь
. Здесь 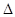 - определитель основной, квадратной матрицы СЛАУ, определитель
- определитель основной, квадратной матрицы СЛАУ, определитель 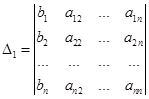 получен из определителя
получен из определителя 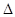 заменой 1-го столбца столбцом свободных членов. Аналогично определитель
заменой 1-го столбца столбцом свободных членов. Аналогично определитель 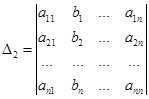 получен из определителя
получен из определителя 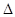 заменой 2-го столбца столбцом свободных членов и т. д.
заменой 2-го столбца столбцом свободных членов и т. д.
2. Теорема 1. (Крамер, Швейцария, 1704-1752) СЛАУ (1), определитель которой не равен 0, имеет единственное решение, определяемое формулами 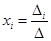 ,
,  .
.
3. Доказательство. Умножим 1-е уравнение системы (1) на алгебраическое дополнение к элементу 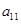 матрицы
матрицы  - число
- число 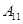 .Коэффициент при
.Коэффициент при  равен
равен 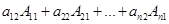 , т. е. он равен разложению по 1-му столбцу того же определителя, в котором первый столбец заменен вторым столбцом. Но определитель с двумя равными столбцами равен 0. Аналогично коэффициенты при
, т. е. он равен разложению по 1-му столбцу того же определителя, в котором первый столбец заменен вторым столбцом. Но определитель с двумя равными столбцами равен 0. Аналогично коэффициенты при 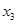 ,…,
,…, 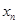 будут равны 0 и мы приходим к соотношению
будут равны 0 и мы приходим к соотношению 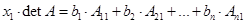 . Правая часть равна
. Правая часть равна 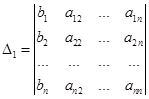 . Тем самым справедлива формула
. Тем самым справедлива формула  . Остальные из доказываемых формул выводятся аналогично.
. Остальные из доказываемых формул выводятся аналогично.
Матричный метод решения СЛАУ
Рассмотрим СЛАУ, в которой число уравнений совпадает с числом неизвестных, и запишем ее в виде 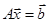 . Если определитель основной матрицы этой системы отличен от 0, то существует обратная матрица
. Если определитель основной матрицы этой системы отличен от 0, то существует обратная матрица  , причем
, причем 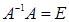 . Умножим обе части равенства
. Умножим обе части равенства 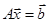 слева на
слева на  и получим равенство
и получим равенство 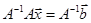 . Так как первые 2 сомножителя в левой части этого уравнения равны единичной матрице и тем самым сокращаются, то мы приходим к формуле
. Так как первые 2 сомножителя в левой части этого уравнения равны единичной матрице и тем самым сокращаются, то мы приходим к формуле
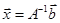 . (2)
. (2)
Метод Гаусса решения СЛАУ
Рассмотрим СЛАУ с произвольным числом уравнений и произвольным числом неизвестных
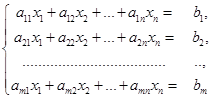 (3)
(3)
и соответствующую расширенную матрицу 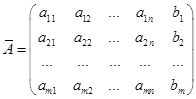 . (4)
. (4)
6. Определение 1. элементарные преобразования над строками матрицы:
1) перемена местами 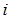 -й и
-й и  -й строк матрицы,
-й строк матрицы,
2) умножение 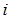 -й строки матрицы на число
-й строки матрицы на число 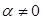 ,
,
3) прибавление к 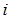 -й строке матрицы
-й строке матрицы  -й строки, умноженной на число
-й строки, умноженной на число 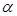 ,
,
4) вычеркивание нулевой троки матрицы.
7. Теорема 2. Элементарные преобразования над строками расширенной матрицы не меняют множества решений соответствующей СЛАУ.
8. Доказательство. Относительно операций 1), 2), 4) утверждение является очевидным.
Преобразование № 3. Установим, что оно не уменьшает множество решений соответствующего СЛАУ: если числа 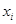 ,
, 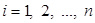 являются решением СЛАУ, то при подстановке этих чисел верным является каждое уравнение СЛАУ,=> и после умножения
являются решением СЛАУ, то при подстановке этих чисел верным является каждое уравнение СЛАУ,=> и после умножения  -го уравнения на число
-го уравнения на число 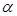 оно остается верным.
оно остается верным.
Геометрический вектор, линейные операции над векторами
9. Определение 1. Геометрические векторы- направленные отрезки, которые считаются равными, если длины отрезков и их направления совпадают, и для которых введены операции сложения векторов и умножения вектора на число по следующим правилам:
10. Введенные операции обладают свойствами: 1)  - коммутативность, 2)
- коммутативность, 2) 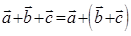 - ассоциативность, 3)
- ассоциативность, 3) 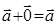 - существование нулевого элемента, 4)
- существование нулевого элемента, 4) 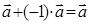 существование противоположного элемента
существование противоположного элемента 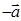 , 5)
, 5) 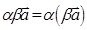 , 6)
, 6) 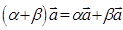 дистрибутивность для числовых коэффициентов, 7)
дистрибутивность для числовых коэффициентов, 7)  - дистрибутивность для векторов, 8)
- дистрибутивность для векторов, 8) 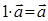 .
.
Лекция №7!
1. Заданы векторы 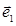 ,
, 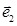 ,…,
,…, 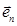 векторного пространства и числа
векторного пространства и числа 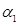 ,
,  ,…,
,…, 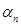 . Величина
. Величина 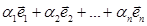
2. числа 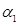 ,
,  ,…,
,…, 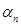 называются коэффициентами линейной комбинации
называются коэффициентами линейной комбинации
3. Теорема 1. Любые 2 не коллинеарных вектора на плоскости линейно независимы, причем любой третий вектор является их линейной комбинацией.
4. Теорема 2. Любые 3 не компланарных вектора на плоскости линейно независимы, причем любой четвертый вектор является их линейной комбинацией.
5. Доказательство теорем 1 и 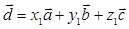 и
и 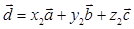 . Их разность дает соотношение
. Их разность дает соотношение 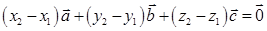

6. Пусть в некотором линейном пространстве векторы 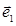 ,
, 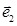 ,…,
,…, 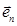 образуют базис и заданы вектора
образуют базис и заданы вектора 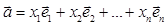 и
и  . над векторами выполнены равенства
. над векторами выполнены равенства 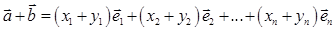 ,
,  ,
, 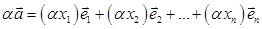 .
.
7. Пусть в реальном пространстве задан вектор 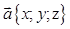 , тогда его длина может быть найдена по формуле
, тогда его длина может быть найдена по формуле 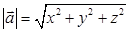 .направляющий вектор
.направляющий вектор 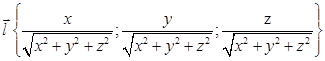 единичной длины с тем же направлением. Вектор-
единичной длины с тем же направлением. Вектор- 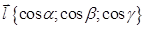 , где
, где 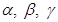 - углы между вектором
- углы между вектором 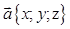 и осями координат. Сами величины
и осями координат. Сами величины 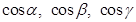 -направляющие косинуса вектора
-направляющие косинуса вектора 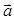 .
.
8. Справедливы следующие свойства скалярного произведения:
1) 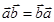
2) 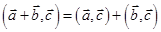
3) 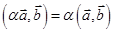
4)  ,
, 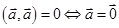 .
.
9. Теорема 3. Проекция линейной комбинации векторов  и
и 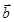 на вектор
на вектор 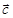 равна линейной комбинации проекций векторов
равна линейной комбинации проекций векторов  и
и 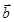 на вектор
на вектор 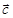 .
.
10. Доказательство. 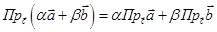 .
.  . Кроме того,
. Кроме того, 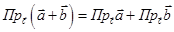 . Теорема доказана.
. Теорема доказана.
11. Заметим, что:
 ,
,
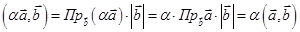 .
.
Лекция №8!
1. Теорема 1. В декартовой системе координат скалярное произведение геометрических векторов равно сумме попарных произведений их координат.
2. Доказательство. Рассмотрим скалярное произведение векторов 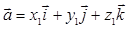 и
и 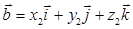 , заданных в декартовой системе координат
, заданных в декартовой системе координат 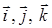 . Используя свойства скалярного произведения векторов, запишем следующие преобразования:
. Используя свойства скалярного произведения векторов, запишем следующие преобразования:
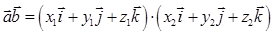
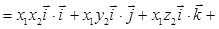
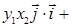

3. Справедливы следующие свойства векторного произведения:
1)  ; 2)
; 2)  ;
;
3) 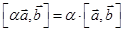 ; 4)
; 4) 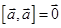 .
.
4. Теорема 2. В декартовой системе координат векторное произведение геометрических пространственных векторов 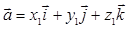 и
и 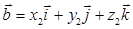 равно вектору
равно вектору 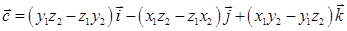 .
.
5. Доказательство. векторное произведение 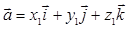 и
и 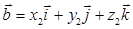 , заданных в декартовой системе координат
, заданных в декартовой системе координат 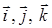 . Используя свойства 2), 3), запишем следующие преобразования:
. Используя свойства 2), 3), запишем следующие преобразования:
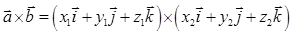
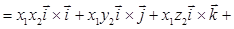
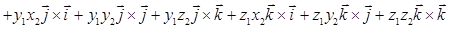 .
.
Для получения заключительного результата заметим, что 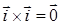 ,
, 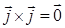 ,
, 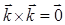 . Кроме того, из правой ориентации базисных векторов
. Кроме того, из правой ориентации базисных векторов 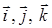 следует, что
следует, что 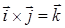 ,
, 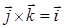 ,
, 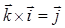 ,
, 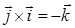 ,
, 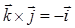 ,
,  . получаем, что
. получаем, что 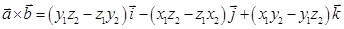 . Теорема доказана.
. Теорема доказана.
Полученный результат можно записать в виде 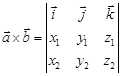 .В декартовой системе координат векторное произведение геометрических пространственных векторов
.В декартовой системе координат векторное произведение геометрических пространственных векторов  и
и  равно вектору, порождаемому определителем, у которого первая строка состоит из базисных векторов
равно вектору, порождаемому определителем, у которого первая строка состоит из базисных векторов 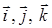 ; вторая строка состоит из координат вектора
; вторая строка состоит из координат вектора  ; третья строка состоит из координат вектора
; третья строка состоит из координат вектора  .
.
6. Теорема 3. Смешанное произведение упорядоченной тройки некомпланарных векторов 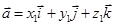 ,
, 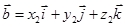 и
и 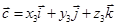 равно объему параллелепипеда, построенного на этих векторах, и взятому со знаком «
равно объему параллелепипеда, построенного на этих векторах, и взятому со знаком «  », если тройка векторов – правая, и взятому со знаком «
», если тройка векторов – правая, и взятому со знаком « 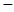 », если тройка векторов – левая.
», если тройка векторов – левая.
7. Доказательство. заданы векторы  ,
,  ,
, 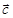 . Векторное
. Векторное
произведение векторов 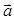 и и 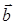 - вектор, перпендикулярный плоскости векторов - вектор, перпендикулярный плоскости векторов  , ,  , равный по длине площади параллелограмма, построенного на этих векторах. , равный по длине площади параллелограмма, построенного на этих векторах. | 8. 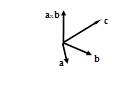 |
Скалярное произведение векторов  и
и 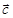 . Векторы
. Векторы  ,
,  и вектор
и вектор  образуют правую тройку векторов => векторы
образуют правую тройку векторов => векторы  ,
,  ,
, 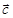 также образуют правую тройку векторов, векторы
также образуют правую тройку векторов, векторы  и
и 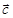 образуют острый угол и их скалярное произведение положительно. (Иначе оно отрицательно.)
образуют острый угол и их скалярное произведение положительно. (Иначе оно отрицательно.) 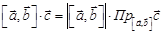 . Смешанное
. Смешанное  ,
,  ,
, 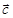 по модулю равно произведению площади основания параллелепипеда
по модулю равно произведению площади основания параллелепипеда 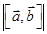 (параллелограмма, построенного на векторах
(параллелограмма, построенного на векторах  ,
,  ) на высоту
) на высоту 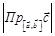 к этому основанию. Теорема доказана.
к этому основанию. Теорема доказана.
9. Теорема 5. Уравнение 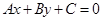 (1) при условии
(1) при условии 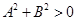 является общим уравнением прямой на плоскости.
является общим уравнением прямой на плоскости.
10. Доказательство. Задано уравнение (1). Условие 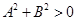 означает, что хотя бы одно из чисел
означает, что хотя бы одно из чисел  отличен от 0. Роль этих коэффициентов симметрична, поэтому для определенности будем считать, что
отличен от 0. Роль этих коэффициентов симметрична, поэтому для определенности будем считать, что 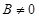 . => при выполнении условия (1) выполняется условие
. => при выполнении условия (1) выполняется условие 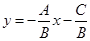 . Возьмем произвольное число
. Возьмем произвольное число 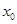 и вычислим
и вычислим 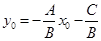 . => для точки
. => для точки 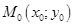 выполнено соотношение
выполнено соотношение 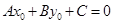 . Вычитая это соотношение из уравнения (1), получим эквивалентное (1) уравнение на плоскости
. Вычитая это соотношение из уравнения (1), получим эквивалентное (1) уравнение на плоскости  (2)
(2)
Уравнение  (3) уравнение прямой в отрезках.
(3) уравнение прямой в отрезках.
Уравнение 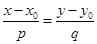 (4) каноническое уравнение прямой на плоскости.
(4) каноническое уравнение прямой на плоскости.
11. Пусть заданы 2 точки: 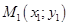 и
и 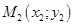 . Очевидно, что уравнение прямой, проходящей через эти две точки, запишется в виде
. Очевидно, что уравнение прямой, проходящей через эти две точки, запишется в виде  (4/).
(4/).
12. Система уравнений вида 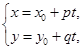
 (5) параметрическое уравнение прямой на плоскости.
(5) параметрическое уравнение прямой на плоскости.
Уравнение  (
(  ) (6) называется нормированным уравнением прямой на плоскости.
) (6) называется нормированным уравнением прямой на плоскости. 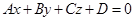 (7) при условии
(7) при условии 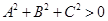 является общим уравнением плоскости.
является общим уравнением плоскости.
13. Уравнение 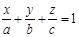 (9) называется уравнением плоскости в отрезках.
(9) называется уравнением плоскости в отрезках.
14. 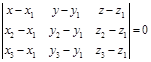 (10) является уравнением плоскости, проходящей через 3 заданные точки
(10) является уравнением плоскости, проходящей через 3 заданные точки 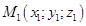 ,
, 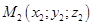 ,
, 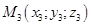 , не лежащие на одной прямой.
, не лежащие на одной прямой.
Аналогично, уравнение 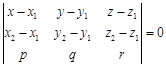 (11) является уравнением плоскости, проходящей через 2 заданные точки
(11) является уравнением плоскости, проходящей через 2 заданные точки 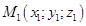 ,
, 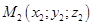 параллельно вектору
параллельно вектору 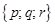 , не коллинеарному вектору
, не коллинеарному вектору  .
.
Также уравнение 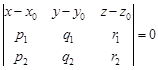 (12) является уравнением плоскости, проходящей через заданную точки
(12) является уравнением плоскости, проходящей через заданную точки 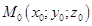 параллельно двум не коллинеарным векторам
параллельно двум не коллинеарным векторам 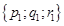 и
и 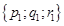 .
.
Уравнение  (
(  ,
, 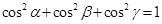 ) (13) называется нормированным уравнением плоскости. Уравнение (13) является уравнением плоскости, удаленной на расстояние
) (13) называется нормированным уравнением плоскости. Уравнение (13) является уравнением плоскости, удаленной на расстояние  от начала координат.
от начала координат.
Лекция №9!
1.  . Т. к. разложение вектора по базису единственное, то
. Т. к. разложение вектора по базису единственное, то 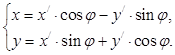 Подставив эти выражения в уравнение (1), мы получим уравнение этой кривой 2-го порядка в новой системе координат
Подставив эти выражения в уравнение (1), мы получим уравнение этой кривой 2-го порядка в новой системе координат 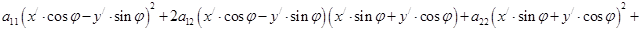
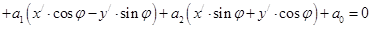 . Если это уравнение записать в виде
. Если это уравнение записать в виде 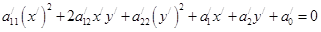 и несложно найти коэффициент
и несложно найти коэффициент 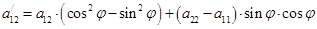 .
.
2. Уравнение 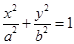 (2) называется каноническим уравнением эллипса. Уравнение
(2) называется каноническим уравнением эллипса. Уравнение  (3) называется каноническим уравнением гиперболы. Уравнение
(3) называется каноническим уравнением гиперболы. Уравнение 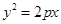 (4) называется каноническим уравнением параболы.
(4) называется каноническим уравнением параболы.
3. Теорема 1. Пусть заданы числа 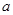 и и 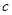 , такие что , такие что  . Точками . Точками 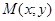 , сумма расстояний от которых до точек , сумма расстояний от которых до точек 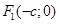 и и 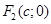 равна равна 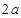 , являются те и только те точки, координаты которых удовлетворяют уравнению (2), где , являются те и только те точки, координаты которых удовлетворяют уравнению (2), где  . . | 4. 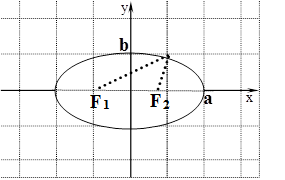 |
5. Доказательство. Расстояние от точки 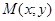 до точки
до точки 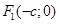 равно
равно 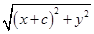 , расстояние от точки
, расстояние от точки 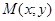 до точки
до точки 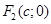 равно
равно 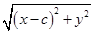 . Следовательно, заданными точками являются те и только те точки, для координат которых выполнено условие
. Следовательно, заданными точками являются те и только те точки, для координат которых выполнено условие 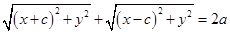 . Перенесем второе слагаемое вправо и возведем обе части соотношения в квадрат, получив
. Перенесем второе слагаемое вправо и возведем обе части соотношения в квадрат, получив  - равносильное уравнение. Отсюда
- равносильное уравнение. Отсюда 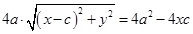 или
или  . Еще раз возведем обе неотрицательные части в квадрат и получим равносильное уравнение
. Еще раз возведем обе неотрицательные части в квадрат и получим равносильное уравнение  или
или 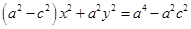 . После деления на правую часть мы приходим к «нужному» уравнению
. После деления на правую часть мы приходим к «нужному» уравнению 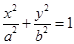 , где
, где 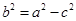 . Теорема доказана.
. Теорема доказана.
эксцентриситет, равный  . Классической характеристикой является директриса – прямая, лежащая в плоскости конического сечения и такая, что отношение расстояний от любой точки кривой до соответствующего фокуса и до директрисы равно эксцентриситету. Для эллипса это две прямые
. Классической характеристикой является директриса – прямая, лежащая в плоскости конического сечения и такая, что отношение расстояний от любой точки кривой до соответствующего фокуса и до директрисы равно эксцентриситету. Для эллипса это две прямые 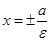 .
.
Эллипс можно представить как единичную окружность, растянутую в 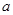 раз вдоль оси абсцисс и в
раз вдоль оси абсцисс и в 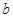 раз вдоль оси ординат.
раз вдоль оси ординат.
уравнение эллипса 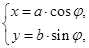
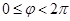 .
.
6. Теорема 2. Пусть заданы числа 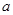 и и 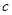 , такие что , такие что  . Точками . Точками 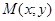 , разность расстояний от которых до точек , разность расстояний от которых до точек 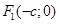 и и 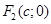 равна равна 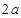 , являются те и только те точки, координаты которых удовлетворяют уравнению (3), где , являются те и только те точки, координаты которых удовлетворяют уравнению (3), где  . . | 7.  |
8. Доказательство. Расстояние от точки 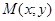 до точки
до точки 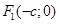 равно
равно 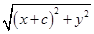 , расстояние от точки
, расстояние от точки 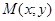 до точки
до точки 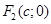 равно
равно 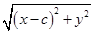 . Следовательно, заданными точками являются те и только те точки, для координат которых выполнено условие
. Следовательно, заданными точками являются те и только те точки, для координат которых выполнено условие  . Перенесем второе слагаемое вправо и возведем обе части соотношения в квадрат, получив
. Перенесем второе слагаемое вправо и возведем обе части соотношения в квадрат, получив 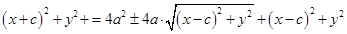 - равносильное уравнение. Отсюда
- равносильное уравнение. Отсюда  или
или  . Еще раз возведем обе неотрицательные части в квадрат и получим равносильное уравнение
. Еще раз возведем обе неотрицательные части в квадрат и получим равносильное уравнение  или
или 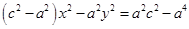 . После деления на правую часть мы приходим к «нужному» уравнению
. После деления на правую часть мы приходим к «нужному» уравнению  , где
, где 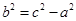 . Теорема доказана.
. Теорема доказана.
В качестве характеристики гиперболы рассматривают эксцентриситет, равный 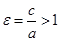 и директриса. Для гиперболы это две прямые
и директриса. Для гиперболы это две прямые 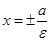 .
.
У канонической гиперболы есть две асимптоты 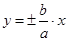 , т. е. прямые, к которым график функции неограниченно приближается при удалении от начала координат к бесконечности.
, т. е. прямые, к которым график функции неограниченно приближается при удалении от начала координат к бесконечности.
Отметим, что уравнение гиперболы может быть записано в параметрическом виде 
 .
.
9. Теорема 3. Пусть задано число  . Точками . Точками 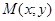 , расстояние от которых до точки , расстояние от которых до точки  равно расстоянию до прямой равно расстоянию до прямой  являются те и только те точки, координаты которых удовлетворяют уравнению (4). являются те и только те точки, координаты которых удовлетворяют уравнению (4). | 10.  |
11. Доказательство. Расстояние от точки 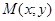 до точки
до точки  равно
равно 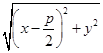 , расстояние от точки
, расстояние от точки 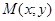 до прямой
до прямой  равно
равно 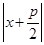 . Следовательно, заданными точками являются те и только те точки, для координат которых выполнено условие
. Следовательно, заданными точками являются те и только те точки, для координат которых выполнено условие 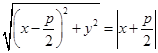 . Возведем обе части соотношения в квадрат и получим
. Возведем обе части соотношения в квадрат и получим 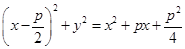 или
или 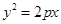 . Теорема доказана.
. Теорема доказана.
У параболы эксцентриситет равен 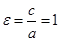 .
.
12. Уравнение 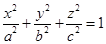 (6) называется каноническим уравнением эллипсоида. эллипс.
(6) называется каноническим уравнением эллипсоида. эллипс.
13. Уравнение 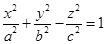 (7) называется каноническим уравнением однополостного гиперболоида. Сечения, перпендикулярные осям абсцисс и ординат, являются гиперболами. эллипсом.
(7) называется каноническим уравнением однополостного гиперболоида. Сечения, перпендикулярные осям абсцисс и ординат, являются гиперболами. эллипсом.
14. Уравнение 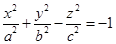 (8) называется каноническим уравнением двуполостного гиперболоида. Сечения, перпендикулярные осям абсцисс и ординат, являются гиперболами. Сечение
(8) называется каноническим уравнением двуполостного гиперболоида. Сечения, перпендикулярные осям абсцисс и ординат, являются гиперболами. Сечение 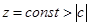 , перпендикулярное оси аппликат, является эллипсом.
, перпендикулярное оси аппликат, является эллипсом.
15. Также отметим уравнения: 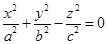 - конуса,
- конуса, 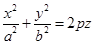 - эллиптического параболоида,
- эллиптического параболоида,  - гиперболического параболоида,
- гиперболического параболоида, 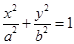 - эллиптического цилиндра,
- эллиптического цилиндра,  -гиперболического цилиндра,
-гиперболического цилиндра, 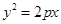 - параболического цилиндра…
- параболического цилиндра…
Лекция №10!
1. Теорема 1. Ограниченное сверху числовое множество имеет точную верхнюю грань. Ограниченное снизу числовое множество имеет точную нижнюю грань.
2. Лемма о вложенных отрезках. (Принцип вложенных отрезков Коши-Кантора или принцип непрерывности Кантора или теорема Кантора о вложенных отрезках) Для любой системы вложенных отрезков  существует хотя бы одна общая точка, принадлежащая всем отрезкам. Такая точка будет единственной, если длины отрезков стремятся к нулю.
существует хотя бы одна общая точка, принадлежащая всем отрезкам. Такая точка будет единственной, если длины отрезков стремятся к нулю.
Ограниченность последовательности, предел числовой последовательности, единственность предела, операции над последовательностями, бесконечно малые величины, свойства б. м., свойства пределов. Вычисление пределов. Бином Ньютона. Число e.
Лекция №11!
1. Теорема 1. Если предел числовой последовательности существует, то он единственный.
2. Доказательство. Доказательство теоремы проведем «методом от противного». Предположим, что теорема неверна и существует, как минимум, 2 числа 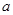 и
и 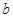 (
( 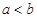 ), для которых выполнены условия определения 2. В этом определении возьмем
), для которых выполнены условия определения 2. В этом определении возьмем  . Тогда, после номера
. Тогда, после номера  члены последовательности отличаются от числа
члены последовательности отличаются от числа 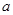 меньше чем на
меньше чем на 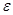 , а после номера
, а после номера 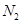 члены последовательности отличаются от числа
члены последовательности отличаются от числа 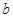 меньше чем на
меньше чем на 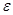 . Покажем, что этого не может быть. В самом деле, при
. Покажем, что этого не может быть. В самом деле, при 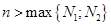 выполнены соотношения
выполнены соотношения  ,
, 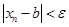 , откуда для этих
, откуда для этих 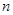 имеем
имеем 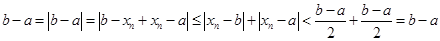 . Теорема доказана.
. Теорема доказана.
3. Теорема 2. Если числовая последовательность имеет предел, то эта числовая последовательность ограничена.
4. Доказательство. Доказательство будет носить конструктивный характер. Возьмем 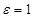 и найдем соответствующее
и найдем соответствующее 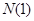 . Разобьем последовательность на 2 части: первые
. Разобьем последовательность на 2 части: первые 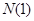 членов и остальные члены последовательности. Первая группа состоит из конечного числа членов и поэтому ограничена. Вторая группа состоит из чисел, удаленных от предельного значения
членов и остальные члены последовательности. Первая группа состоит из конечного числа членов и поэтому ограничена. Вторая группа состоит из чисел, удаленных от предельного значения 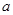 не больше чем на 1, и поэтому также ограничена. Объединение двух ограниченных множеств есть множество ограниченное. Теорема доказана.
не больше чем на 1, и поэтому также ограничена. Объединение двух ограниченных множеств есть множество ограниченное. Теорема доказана.
5. Теорема 5. Числовая последовательность 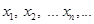 имеет предел, равный
имеет предел, равный 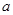 тогда и только тогда, когда последовательность
тогда и только тогда, когда последовательность 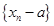 ,
, 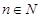 является бесконечно малой величиной.
является бесконечно малой величиной.
6. Доказательство. Пусть 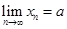 , т.е. при для каждого
, т.е. при для каждого  при
при 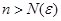 выполнено неравенство
выполнено неравенство 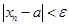 (
( 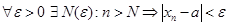 ). Но это неравенство равносильно тому, что
). Но это неравенство равносильно тому, что 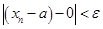 , т. е. последовательность
, т. е. последовательность 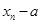 ,
, 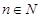 имеет предел 0, т.е. является бесконечно малой величиной. Теорема доказана.
имеет предел 0, т.е. является бесконечно малой величиной. Теорема доказана.
7. Теорема 6. (Свойства пределов) Пусть 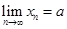 ,
, 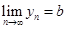 , тогда
, тогда 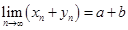 ,
, 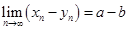 ,
, 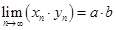 , а если, кроме того,
, а если, кроме того, 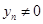 ,
, 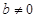 , то
, то 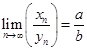 .
.
8. Доказательство. Докажем в условиях теоремы формулу 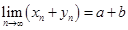 , т. е. мы докажем, что предел суммы последовательностей равен сумме их пределов, если каждый из пределов существует. Так как
, т. е. мы докажем, что предел суммы последовательностей равен сумме их пределов, если каждый из пределов существует. Так как 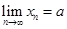 , то
, то 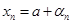 , где
, где 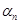 - б. м. Аналогично
- б. м. Аналогично 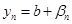 , где
, где 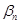 - б. м. Отсюда следует, что
- б. м. Отсюда следует, что 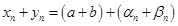 . В последней скобке сумма двух бесконечно малых величин есть величина б. м. Поэтому
. В последней скобке сумма двух бесконечно малых величин есть величина б. м. Поэтому  представляется в виде суммы
представляется в виде суммы  и бесконечно малой величины
и бесконечно малой величины 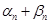 . В силу теоремы 5 это означает, что
. В силу теоремы 5 это означает, что 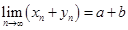 . Первое утверждение теоремы доказана. Формула
. Первое утверждение теоремы доказана. Формула 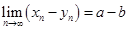 доказывается совершенно аналогично. Рассмотрим теперь формулу
доказывается совершенно аналогично. Рассмотрим теперь формулу 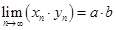 и используем для преобразования левой части те же обозначения. Поэтому
и используем для преобразования левой части те же обозначения. Поэтому 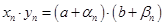 …
…
