Общий вид транспортной матрицы
Пункты отправления,  | Пункты потребления,  | Запасы, ед. прод. | |||
 |  | … |  | ||
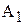 |  , [руб./ед. прод.] , [руб./ед. прод.] |  | … |  |  |
 |  |  | … |  |  |
| … | … | … | … | … | … |
 |  |  | … |  |  |
| Потребность ед. прод. |  |  | … |  |  |
Из модели (4.1) следует, что сумма запасов продукции во всех пунктах отправления должна равняться суммарной потребности во всех пунктах потребления, т.е.
 . . | (4.2) |
Если (4.2) выполняется, то ТЗ называется сбалансированной (закрытой), в противном случае – несбалансированной(открытой). В случае, когда суммарные запасы превышают суммарные потребности, необходим дополнительный фиктивный (реально не существующий) пункт потребления, который будет формально потреблять существующий излишек запасов, т.е.
 .
.
Если суммарные потребности превышают суммарные запасы, то необходим дополнительный фиктивный пункт отправления, формально восполняющий существующий недостаток продукции в пунктах отправления:
 .
.
Для фиктивных перевозок вводятся фиктивныетарифы  , величина которых обычно приравнивается к нулю
, величина которых обычно приравнивается к нулю  . Но в некоторых ситуациях величину фиктивного тарифа можно интерпретировать как штраф, которым облагается каждая единица недопоставленной продукции. В этом случае величина
. Но в некоторых ситуациях величину фиктивного тарифа можно интерпретировать как штраф, которым облагается каждая единица недопоставленной продукции. В этом случае величина  может быть любым положительным числом.
может быть любым положительным числом.
Задача о назначениях – частный случай ТЗ. В задаче о назначениях количество пунктов отправления равно количеству пунктов назначения. Объемы потребности и предложения в каждом из пунктов назначения и отправления равны 1. Примером типичной задачи о назначениях является распределение работников по различным видам работ, минимизирующее суммарное время выполнения работ.
Переменные задачи о назначениях определяются следующим образом

Методические рекомендации
Стандартная транспортная задача
Задача №4.01
Заводы некоторой автомобильной фирмы расположены в городах А, В и С. Основные центры распределения продукции сосредоточены в городах D и E. Объемы производства указанных трех заводов равняются 1000, 1300 и 1200 автомобилей ежеквартально. Величины квартального спроса в центрах распределения составляют 2300 и 1400 автомобилей соответственно. Стоимости перевозки автомобилей по железной дороге по каждому из возможных маршрутов приведены в табл.4.2.
Таблица 4.2
Стоимость перевозки автомобилей, руб./шт.
| D | E | |
| А | ||
| В | ||
| С |
Постройте математическую модель, позволяющую определить количество автомобилей, перевозимых из каждого завода в каждый центр распределения, таким образом, чтобы общие транспортные расходы были минимальны.
Решение
Определение переменных
Обозначим количество автомобилей, перевозимых из i-го завода в j-й пункт потребления через 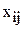 .
.
Проверка сбалансированности задачи
Проверим равенство суммарного производства автомобилей и суммарного спроса

откуда следует вывод – задача несбалансирована, поскольку спрос на автомобили превышает объем их производства. Для установления баланса введем дополнительный фиктивный завод с ежеквартальным объемом производства 200 шт. (  ). Фиктивные тарифы
). Фиктивные тарифы  приравняем к нулю (т.к. перевозки в действительности производиться не будут).
приравняем к нулю (т.к. перевозки в действительности производиться не будут).
Построение транспортной матрицы
Согласно результатам проверки сбалансированности задачи №4.01 в транспортной матрице должно быть четыре строки, соответствующих заводам и два столбца, соответствующих центрам распределения (см. табл.4.3). Тариф перевозки обычно вписывают в правом нижнем углу клетки матрицы для удобства дальнейшего нахождения опорных планов задачи.
Таблица 4.3
