Правила Саррюса (правило треугольников)
ОДОБРЕНО
Протокол заседания ПЦМК
по математике
№ 2 от 29.09.2013
СБОРНИК МЕТОДИЧЕСКИХ УКАЗАНИЙ
ДЛЯ ОБУЧАЮЩИХСЯ ПО ВЫПОЛНЕНИЮ
ПРАКТИЧЕСКИХ ЗАНЯТИЙ
ДИСЦИПЛИНА «ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ»
специальность 230115 ПРОГРАММИРОВАНИЕ В КОМПЬЮТЕРНЫХ СИСТЕМАХ
Актуализировал
преподаватель
ГБОУ СПО «ПГК»
Афонина Н.Е.
Самара, 2013г.
Раздел «ОСНОВЫ ЛИНЕЙНОЙ АЛГЕБРЫ»
Тема «МАТРИЦА И ОПРЕДЕЛИТЕЛЬ»
Практическое занятие №1:
«ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЕЙ»
Учебная цель:формировать умение вычислять определители 2-го, 3-го и n-го порядка.
Учебные задачи:
1. научиться вычислять определитель 2-го порядка;
2. научиться вычислять определитель 3-го порядка;
3. научиться определять определитель n-го порядка;
4. научиться применять свойства при вычислении определителей.
Образовательные результаты, заявленные во ФГОС третьего поколения
Студент должен
уметь:
- решать системы линейных уравнений;
знать:
- основные понятия линейной алгебры.
Задачи практического занятия №1
- Повторить теоретический материал по теме практического занятия.
- Ответить на вопросы для закрепления теоретического материала.
- Изучить методические рекомендации по выполнению работы.
- Выполнить задания на нахождение вычисление определителей.
- Оформить отчет.
Обеспеченность занятия (средства обучения):
1. Справочная литература:
- Сборник задач по высшей математике для экономистов: Учебное пособие / Под ред. В.И.Ермакова. – М.: ИНФРА-М, 2005. – 575 с.
2. Рабочие тетради: тетради для практических занятий в клетку.
3. Калькулятор: простой.
4. Ручка.
Краткие теоретические и учебно-методические материалы
По теме практического занятия
Определитель матрицы второго порядка называется число
.
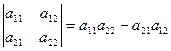Определитель матрицы третьего порядка называется число
.
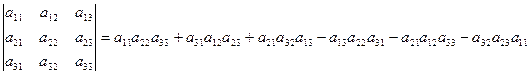Минором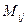 
элемента 
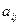определителя n-го порядка называется определитель (n-1)-го порядка, который получается в результате вычёркивания в определителе n-го порядка строки и столбца, содержащих элемент .
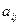Алгебраическим дополнением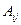 
элемента 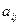называется его минор, умноженный на 
: 
.
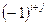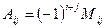Разложение определителя по элементам ряда. Определитель равен сумме произведений элементов любой его строки (столбца) на их алгебраические дополнения, т.е.
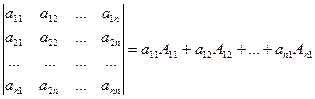
или
.
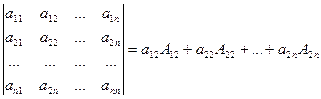Если в определителе все элементы ряда, кроме одного, равны нулю, то определитель равен произведению отличного от нуля элемента на его алгебраическое дополнение, т.е.
.
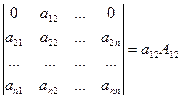Правила Саррюса (правило треугольников).
Три слагаемых, входящих в сумму со знаком «плюс», находятся следующим образом: одно слагаемое состоит из произведения элементов, расположенных на главной диагонали, два других – произведения элементов, лежащих на параллели к этой диагонали с добавлением третьего множителя из противоположного угла. (Получается два треугольника, вершинами которых являются перемножаемые элементы.) (рис. 1).
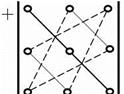
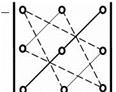
Рис.1 Рис.2
Слагаемые, входящие в сумму со знаком «минус», строятся таким же образом относительно побочной диагонали. (рис.2).
Свойства определителей:
1. При замене каждой строки определителя столбцом с тем же самым номером значение определителя не изменяется.
2. Общий множитель всех элементов ряда определителя можно вынести за знак определителя.
3. Определитель, содержащий две одинаковые строки (столбца), равен нулю.
4. Определитель не изменяется, если к элементам одной из его строк (столбцов) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.
5. Если каждый элемент какого-либо столбца определителя представлен в виде суммы двух слагаемых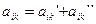 
, то этот определитель равен сумме двух определителей, у которого k-й столбец первого определителя состоит из элементов 
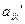, а k-й столбец второго – из элементов 
.
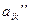Вопросы для закрепления теоретического материала к практическому занятию:
1. Что называется определителем второго порядка?
2. Что называется определителем третьего порядка?
3. Что такое минор элемента определителя?
4. Что такое алгебраическое дополнение элемента определителя?
5. Сформулируйте правило Саррюса.
6. Сформулируйте свойства определителей.
7. Каким образом можно найти определитель 4 порядка?