Т.е. условная вероятность совпадает с безусловной
Для произведения независимых событий А и В получаем равенство
Р(АВ)=Р(А|В)Р(В)=Р(А)Р(В),
которое озвучивается так: вероятность произведения двух независимых событий равна произведению их вероятностей. Это равенство может быть также использовано в качестве определения независимости случайных событий.
Если А не зависит от В, т.е. Р(А|В)= Р(А), тогда и В не зависит от А, что доказывается цепочкой простых преобразований
Р(В|А) =  =
=  =
=  =
=  = Р(В).
= Р(В).
Примеры независимости случайных событий дают эксперименты с бросанием кубика или монеты, в которых одни и те же события в разное время происходят с одной и той же вероятностью, т.е. вероятности событий - постоянные величины:
Р( 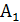 =”утром выпал орел”)= Р(
=”утром выпал орел”)= Р( 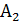 =”вечером выпал орел”)= Р(
=”вечером выпал орел”)= Р( 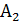 |
| 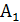 )=
)=  .
.
Рассмотренную выше парную независимость случайных событий следует отличать от независимости в совокупности. Случайные события называются независимыми в совокупности, если они попарно независимы и каждое из них не зависит от произведения любого набора из остальных событий. В случае независимости событий в совокупности вероятность их произведения равна произведению вероятностей:
Р( 
Пример. Стрелок попадает в мишень с вероятностью 0,6. Какова вероятность хотя бы одного попадания в серии из трех выстрелов?
Обозначим  - попадание в мишень при
- попадание в мишень при 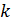 -й попытке. Поскольку попадание и промах образуют полный набор событий, то промах -
-й попытке. Поскольку попадание и промах образуют полный набор событий, то промах -  имеет вероятность Р(
имеет вероятность Р(  ) = 1-
) = 1-  Событие А = “хотя бы одно попадание” противоположно событию В = “три промаха”, которое в принятой системе обозначений представляется в виде В=
Событие А = “хотя бы одно попадание” противоположно событию В = “три промаха”, которое в принятой системе обозначений представляется в виде В=  , т.е. А=
, т.е. А= 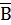 . Поскольку
. Поскольку  =
=  = В, то А + В = Ω. Далее, промахи
= В, то А + В = Ω. Далее, промахи  независимы в совокупности, т.к. в соответствии с условиями задачи их вероятность постоянна (не зависит от промахов в других выстрелах). Эти факты позволяют вычислить искомую вероятность события следующим образом:
независимы в совокупности, т.к. в соответствии с условиями задачи их вероятность постоянна (не зависит от промахов в других выстрелах). Эти факты позволяют вычислить искомую вероятность события следующим образом:
Р(А) = 1- Р(В) = 1-  = 1-
= 1-  = 0,936.
= 0,936.
Необходимо отметить, что проверить решение данной задачи с помощью числовой таблицы в соответствии с классической схемой не позволяет то обстоятельство, что попадания и промахи неравновозможны.
2.10. Формула полной вероятности
Пусть случайные события  попарнонесовместны и событиеА содержится в их суммеАÌ
попарнонесовместны и событиеА содержится в их суммеАÌ  , тогда справедлива формула полной вероятности
, тогда справедлива формула полной вероятности
Р(А)=  .
.
В данных условиях событие А можно представить в виде
А=А(  ) или А=
) или А=  .
.
В силу попарной несовместности событий 
 =∅ при
=∅ при  ≠
≠  ) имеет место попарная несовместность событий А
) имеет место попарная несовместность событий А  , т.к.
, т.к.  (А
(А 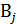 )=(А
)=(А  )(
)( 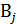 А)=А
А)=А  А=А(
А=А(  )А=А∅А=∅. Далее, учитывая, что Р(
)А=А∅А=∅. Далее, учитывая, что Р(  )=Р(
)=Р(  )Р(
)Р(  ) окончательно находим
) окончательно находим
Р(А)=Р(  )=
)=  .
.
События  интерпретируются как условия наступления события А и называются предпосылками события А. События предпосылки принято называть гипотезами. Их вероятности известны до опыта и потому называются априорными. Теперь формулу полной вероятности можно трактовать следующим образом: вероятность любого события разлагается в сумму вероятностей гипотез, взятых с коэффициентами равными условным вероятностям данного события относительно этих гипотез.
интерпретируются как условия наступления события А и называются предпосылками события А. События предпосылки принято называть гипотезами. Их вероятности известны до опыта и потому называются априорными. Теперь формулу полной вероятности можно трактовать следующим образом: вероятность любого события разлагается в сумму вероятностей гипотез, взятых с коэффициентами равными условным вероятностям данного события относительно этих гипотез.
При решении задач для обеспечения условий применения формулы полной вероятности предпосылки  выбирают попарно несовместными и образующими полный набор, т.е.
выбирают попарно несовместными и образующими полный набор, т.е.  =Ω .
=Ω .
Пример. В первой группе из 20 студентов 5 юношей, а во второй группе из 30 студентов - 3 юноши. Какова вероятность того, что выбранный наугад студент - юноша (событие А)?
Поскольку выбранный студент числится в какой-либо из двух групп, то в качестве гипотез естественно принять его принадлежность первой группе - 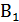 и второй группе -
и второй группе - 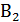 .Вероятности гипотез найдем исходя из доли численности групп в общем количестве студентов:
.Вероятности гипотез найдем исходя из доли численности групп в общем количестве студентов:
Р( 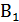 )=
)=  =
=  , Р(
, Р( 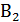 )=
)=  =
=  .
.
Затем найдем соответствующие условные вероятности, исходя, на сей раз из доли юношей в каждой группе
 =
=  =
=  ,
,  =
=  =
= 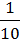 .
.
И, наконец, вычислим окончательный результат
Р(А)=  ·
·  +
+ 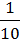 ·
·  =
=  =
=  .
.
Простота задачи позволяет проконтролировать полученное решение с помощью классической схемы. Поскольку выбор производится из совокупности в количестве 50 студентов при наличии в ней 8 юношей, то в соответствии с формулой классической вероятности
Р(А) =  =
=  ,
,
чего и следовало ожидать.
При расчете вероятности сложных событий с использованием формулы полной вероятности схему решения задачи удобно иллюстрировать, систематизировать и анализировать с помощью, так называемого дерева вероятностей, ветви которого описывают все мыслимые сценарии развития каждой возможной начальной ситуации. Для рассмотренной задачи дерево вероятностей будет иметь структуру, изображенную ниже.
| Выбор группы |
Первая 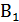  |
Вторая 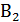 |
| Выбор студента |
| Выбор студента |
Р( 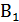 )= )=  |
Р( 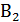 )= )=  |
| юноша |
| юноша |
 = =  |
 = = 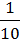 |
 · ·  = = 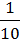 |
 · ·  = =  |
Р(А) =  |
2.11. Формула Байеса
Для событий с предпосылками интересна и такая постановка вопроса: а какова вероятность предпосылки  , если произошло событие А? Чтобы проиллюстрировать данную ситуацию с помощью рассмотренного выше примера переформулируем его следующим образом: найти вероятность того, что выбранный наугад студент учится в первой (или второй) группе, если известно что он - юноша.
, если произошло событие А? Чтобы проиллюстрировать данную ситуацию с помощью рассмотренного выше примера переформулируем его следующим образом: найти вероятность того, что выбранный наугад студент учится в первой (или второй) группе, если известно что он - юноша.
В этой и подобной ей задачах по сути дела требуется найти условную вероятность гипотезы  . Эту вероятность называют апостериорной в отличие от априорной вероятности
. Эту вероятность называют апостериорной в отличие от априорной вероятности  . Апостериорную вероятность находят при условии, что событие А уже произошло, т.е. после опыта. Решение этой задачи обеспечивает формула Байеса.
. Апостериорную вероятность находят при условии, что событие А уже произошло, т.е. после опыта. Решение этой задачи обеспечивает формула Байеса.
Пусть случайные события  попарнонесовместны и событиеА содержится в их суммеАÌ
попарнонесовместны и событиеА содержится в их суммеАÌ  , тогда
, тогда
справедлива формула Байеса
 =
=  , 𝑘=1,2, . . . , n.
, 𝑘=1,2, . . . , n.
Доказательство осуществляется с помощью цепочки простых преобразований с использованием свойства коммутативности произведения событий, определения условной вероятности и формулы полной вероятности:
 =
=  =
=  =
=  =
=  .
.
Теперь можно приступить к решению задачи, сформулированной в начале параграфа.
Итак, требуется найти 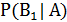 , где событие А=”выбран юноша”. Подставляем в формулу Байеса фигурирующие в ней вероятности, рассчитанные в предыдущем параграфе, и находим нужный ответ:
, где событие А=”выбран юноша”. Подставляем в формулу Байеса фигурирующие в ней вероятности, рассчитанные в предыдущем параграфе, и находим нужный ответ:
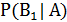 =
= 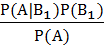 =
=  =
=  =
=  .
.
Простое решение такой задачи с помощью классической схемы не представляется возможным, что лишний раз свидетельствует об ограниченности ее возможностей.
Практикум
Сводка используемых формул:
Р(А+В)=Р(А)+Р(В) для несовместных событий А и В;
Р(А+В)=Р(А)+Р(В)-Р(АВ) для совместных событий А и В;
Р(АВ)=Р(А)Р(В) для независимых событий А и В;
 = Р(А|В)Р(В) в случае зависимости события А от В.
= Р(А|В)Р(В) в случае зависимости события А от В.
Операции над событиями
1. При стрельбе по мишени двух стрелков: А=”попадание в мишень перового стрелка”, В=”попадание в мишень второго стрелка”. Сумма этих событий по определению означает: в мишень попал либо первый стрелок, либо второй стрелок, либо они попали в мишень вместе (одновременно). Иными словами А+В=”попадание в мишень хотя бы одного стрелка”. Эта задача содержательно идентична серии из двух выстрелов одного стрелка. Обозначив А=”попадание в мишень в первом выстреле”, В=”попадание в мишень во втором выстреле” получим А+В=”хотя бы одно попадание в мишень в серии из двух выстрелов”.
Произведение событий в первом и втором случаях дает соответственно АВ=”попадание обоих стрелков”=”два попадания в серии из двух выстрелов” =“попасть дважды”.
2. При извлечении двух шаров из урны в случае  = ”в к-той попытке извлечен белый шар” сумма событий
= ”в к-той попытке извлечен белый шар” сумма событий 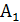 +
+ 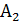 = ”из двух извлеченных из урны шаров хотя бы один - белый ”. Извлечению двух белых шаров отвечает произведение
= ”из двух извлеченных из урны шаров хотя бы один - белый ”. Извлечению двух белых шаров отвечает произведение  .
.
3. В обоих примерах, будь то стрельба по мишени или извлечение шаров из урны, не оговаривается необходимость физически одновременного осуществления испытаний - двух выстрелов или извлечения сразу двух шаров. Тем не менее, произведение событий трактуется как их одновременная реализация, понимаемая как осуществление и одного и другого события вместе. Отсюда сразу же протягивается ниточка к понятию совместности событий.
Ясное дело, что в рассмотренных примерах события А и В являются совместными, поскольку можно дважды попасть в мишень или извлечь два белых шара, если по условию задачи они в урне имеются.
Расчет числа исходов
Расчет количества возможных исходов базируется на основе содержательного анализа постановки решаемой задачи.
1. Определить количество способов упорядочения 8-ми различных объектов.
Различимые объекты можно рассматривать как условно перенумерованные. Поэтому решение задачи сводится к определению числа комбинаций из 8-ми цифр, отличающиеся не только самими цифрами, но и их порядком.
На первое место в комбинации может быть поставлена любая из 8 цифр, на второе любая из 7 оставшихся. При этом любой из 8 способов выбора первой цифры может комбинировать с любым из 7 способов выбора второй цифры и т.д. В итоге получаем внушительное число
N = 8! = 8·7·6·5·4·3·2·1 = 40320.
2. Готовится к выпуску лотерея с шестизначными номерами и трехзначными сериями. Сколько будет билетов всего, если в серии и номере допускаются любые комбинации цифр (в том числе 000, 001 и т.п.) и в каждой серии предусматриваются всевозможные номера?
В серии насчитывается 3 цифры и серия 013 отличается от 103. При наборе серии на первое место может быть поставлена любая цифра из 10, на второе - любая опять-таки из 10 и т.д. Поскольку первая цифра может сочетаться с любыми комбинациями двух последующих цифр, то для числа серий получаем величину  =10·10·10 =
=10·10·10 =  .
.
По тем же соображениям количество номеров в серии  =
=  . По условию задачи столько билетов в каждой серии и потому всего билетов будет
. По условию задачи столько билетов в каждой серии и потому всего билетов будет  =
=  =
=  = 1 млрд, т.е. каждому жителю нашей страны достанется примерно 7 билетов.
= 1 млрд, т.е. каждому жителю нашей страны достанется примерно 7 билетов.
3. Преподаватель из 20 билетов разрешает студенту вытащить сразу 2 билета. Сколькими различными способами это можно сделать?
Из самой постановки задачи абсолютно ясно, что студенту совершенно не важно, какую комбинацию номеров он вытащил (2, 9) или (9, 2) - для него данные комбинации неразличимы, а значение имеет лишь его способность ответить на эти билеты. Это означает, что ответ на поставленный вопрос следует искать с помощью числа сочетаний
N =  =
=  =
=  =
=  = 190.
= 190.
4. Сколькими способами можно распределить 6 различных книг между 3-мя студентами поровну?
Сначала проанализируем постановку задачи. Очевидно, что для студента комбинации одинаковых предметов (химия, философия или философия, химия) неразличимы, т.е. комбинации должны отличаться только составом. Следовательно, при решении задачи следует задействовать число сочетаний. Чтобы установить вид формулы расчета достаточно составить схему дележа парами: первые два произвольно выбранные учебника отдать первому студенту (  =
=  ), вторые два - второму (
), вторые два - второму (  =
=  ), а на долю последнего студента придется оставшаяся пара (
), а на долю последнего студента придется оставшаяся пара (  =
=  = 1). Поскольку каждый набор учебников первого студента может комбинировать со всеми наборами для двух других студентов, то эти числа должны быть взяты в произведении и ответом задачи является
= 1). Поскольку каждый набор учебников первого студента может комбинировать со всеми наборами для двух других студентов, то эти числа должны быть взяты в произведении и ответом задачи является
N =  =
=  =
= 
 =
=  = 90.
= 90.
Однако дележ может быть устроен иначе - по одному учебнику каждому студенту по принципу “тебе-тебе-тебе” в два круга. В соответствии с такой схемой подсчет количества возможных вариантов дележа с учетом сокращения на каждом последующем шаге числа шаров на 1 будет производиться по формуле
N= 6·5·4·3·2·1 = 720.
Этот число существенно превышает верный результат, поскольку последняя схема не учитывает неразличимость комбинаций одного состава.
Таким образом, во избежание ошибок на передний план выдвигается содержательный анализ постановки задачи и построение на его основе алгоритма ее решения.
