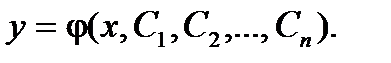Подставляем полученное соотношение в исходное уравнение
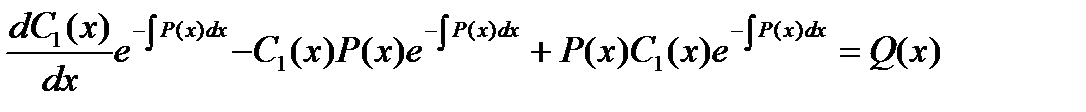
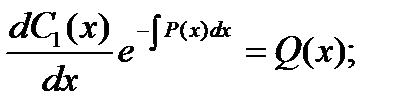
Из этого уравнения определим переменную функцию С1(х):
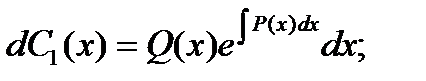
Интегрируя, получаем:
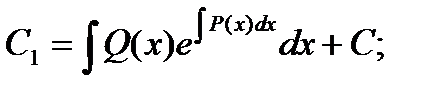
Подставляя это значение в исходное уравнение, получаем:
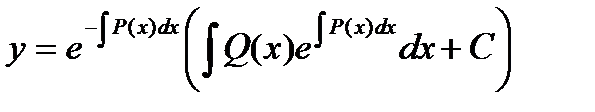 .
.
Таким образом, мы получили результат,
33.Уравнение Бернулли.
Определение. Уравнением Бернуллиназывается уравнение вида
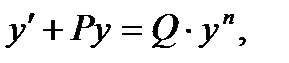 где P и Q – функции от х или постоянные числа, а n – постоянное число, не равное 1.
где P и Q – функции от х или постоянные числа, а n – постоянное число, не равное 1.
Для решения уравнения Бернулли применяют подстановку 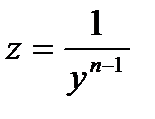 , с помощью которой, уравнение Бернулли приводится к линейному.
, с помощью которой, уравнение Бернулли приводится к линейному.
Для этого разделим исходное уравнение на yn. 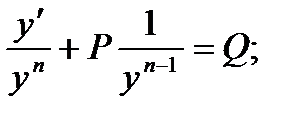 Применим подстановку, учтя, что
Применим подстановку, учтя, что 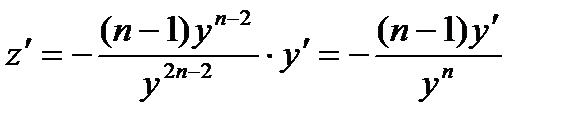 .
. 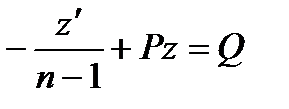
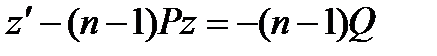 Т.е. получилось линейное уравнение относительно неизвестной функции z. Решение этого уравнения будем искать в виде:
Т.е. получилось линейное уравнение относительно неизвестной функции z. Решение этого уравнения будем искать в виде: 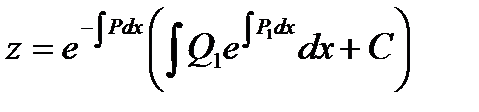
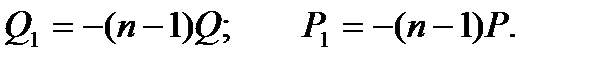
Пример. Решить уравнение 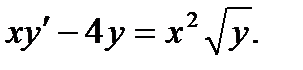
Разделим обе части уравнения на 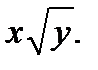
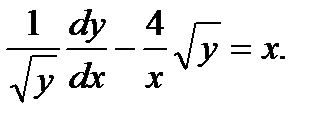
Полагаем 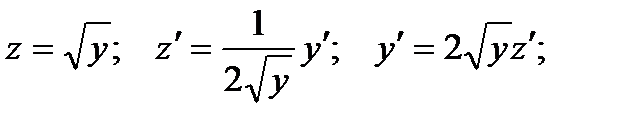
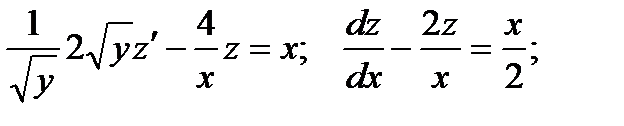
Получили линейное неоднородное дифференциальное уравнение. Рассмотрим соответствующее ему линейное однородное уравнение:
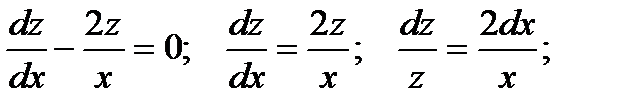
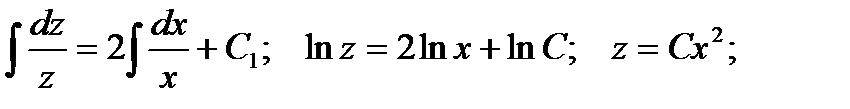
Полагаем C = C(x) и подставляем полученный результат в линейное неоднородное уравнение, с учетом того, что:
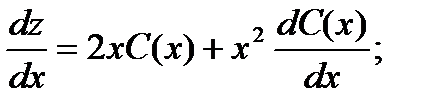
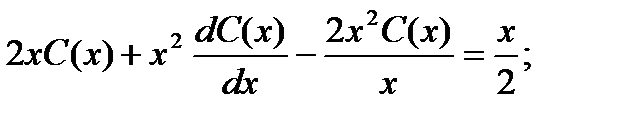
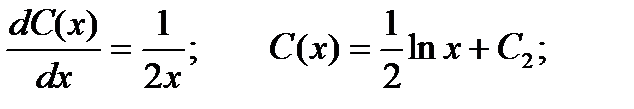
Получаем: 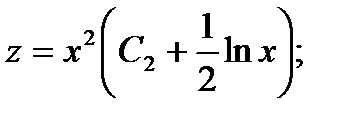
Применяя обратную подстановку, получаем окончательный ответ:
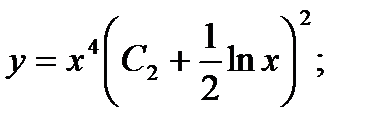
Дифференциальные уравнения высших порядков.
Определение. ДУ порядка n называется уравнение вида: 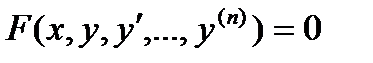 В некоторых случаях это уравнение можно разрешить относительно y(n):
В некоторых случаях это уравнение можно разрешить относительно y(n): 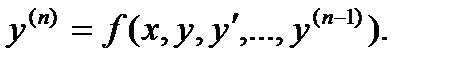 Так же как и уравнение первого порядка, уравнения высших порядков имеют бесконечное количество решений. Определение. Решение
Так же как и уравнение первого порядка, уравнения высших порядков имеют бесконечное количество решений. Определение. Решение 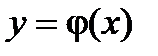 удовлетворяет начальным условиям
удовлетворяет начальным условиям 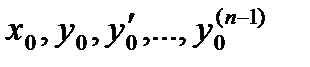 , если
, если  Определение. Нахождение решения уравнения
Определение. Нахождение решения уравнения 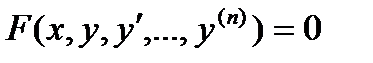 , удовлетворяющего начальным условиям
, удовлетворяющего начальным условиям 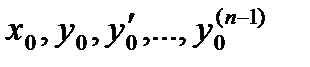 , называется решением задачи Коши. Теорема Коши. Если функция (n-1) –й переменных вида
, называется решением задачи Коши. Теорема Коши. Если функция (n-1) –й переменных вида 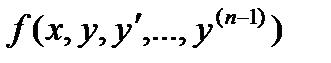 в некоторой области D (n-1)- мерного пространства непрерывна и имеет непрерывные частные производные по
в некоторой области D (n-1)- мерного пространства непрерывна и имеет непрерывные частные производные по 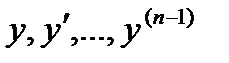 , то какова бы не была точка (
, то какова бы не была точка ( 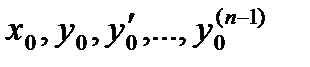 ) в этой области, существует единственное решение
) в этой области, существует единственное решение 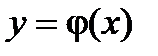 уравнения
уравнения 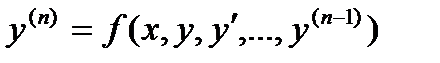 , определенного в некотором интервале, содержащем точку х0, удовлетворяющее начальным условиям
, определенного в некотором интервале, содержащем точку х0, удовлетворяющее начальным условиям 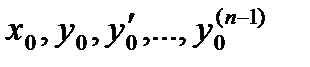 .
.
ДУ высших порядков, решение которых может быть найдено аналитически, можно разделить на несколько основных типов.
Уравнения вида y(n) = f(x). Если f(x) – ф-я непрерывная на некотором промежутке a < x < b, то реш может быть найдено последовательным интегрированием 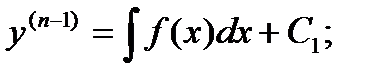
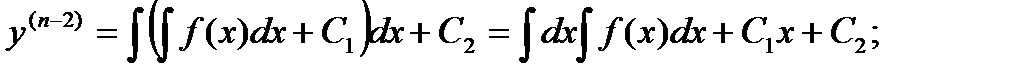
……………………………… 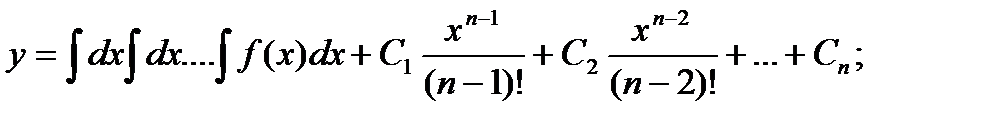
34Уравнения, не содержащие явно искомой функциии ее производных до порядка k – 1 включительно. Это уравнения вида: 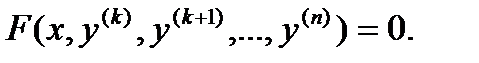 В уравнениях такого типа возможно понижение порядка на k единиц. Для этого производят замену переменной:
В уравнениях такого типа возможно понижение порядка на k единиц. Для этого производят замену переменной: 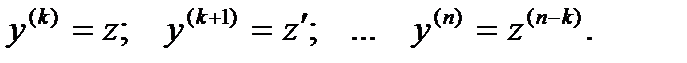
Тогда получаем: 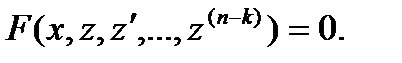 Теперь допустим, что полученное дифференциальное уравнение проинтегрировано и совокупность его решений выражается соотношением:
Теперь допустим, что полученное дифференциальное уравнение проинтегрировано и совокупность его решений выражается соотношением: 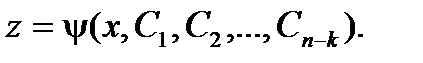 Делая обратную подстановку, имеем:
Делая обратную подстановку, имеем: 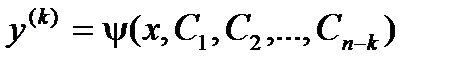 Интегрируя полученное соотношение последовательно k раз, получаем окончательный ответ:
Интегрируя полученное соотношение последовательно k раз, получаем окончательный ответ: