Предел и непрерывность функции многих переменных
 Понятия предела и непрерывности функции нескольких переменных вводятся аналогично понятиям предела и непрерывности функции одной переменной.
Понятия предела и непрерывности функции нескольких переменных вводятся аналогично понятиям предела и непрерывности функции одной переменной.
§ d-окрестностью точки М0(х0;у0) называется множество всех точек М(х;у) плоскости, для которых выполняется условие 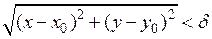 , то есть внутренних точек круга с центром в точке М0 и радиусом d. Множество, состоящее из всех внутренних точек круга, за исключением самой точки М0, называется проколотой d-окрестностью точки М0.
, то есть внутренних точек круга с центром в точке М0 и радиусом d. Множество, состоящее из всех внутренних точек круга, за исключением самой точки М0, называется проколотой d-окрестностью точки М0.
Пусть функция z=f(x;y) определена в некоторой окрестности точки М0(х0;у0), за исключением, может быть, самой этой точки.
§ Число А называется пределом функции z=f(x;y) при 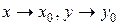 (или при М(х;у)®М0(х0;у0)), если для любого
(или при М(х;у)®М0(х0;у0)), если для любого 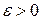 существует
существует 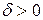 такое, что для всех точек М(х;у) из проколотой d-окрестности точки М0(х0;у0) выполняется неравенство
такое, что для всех точек М(х;у) из проколотой d-окрестности точки М0(х0;у0) выполняется неравенство 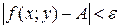 . Обозначают
. Обозначают 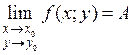 .
.
Из определения следует, что если предел существует, то он не зависит от пути, по которому точка М стремится к точке М0.
Предел функции двух переменных обладает свойствами, аналогичными свойствам предела функции одной переменной, позволяющими вычислять пределы суммы, произведения, отношения функций.
§ Функция z=f(x;y) называется непрерывной в точке М0(х0;у0), если она определена в этой точке и некоторой ее окрестности и имеет предел при М®М0, равный значению функции в этой точке: 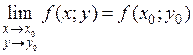
Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области.
Свойства функций, непрерывных в ограниченной замкнутой области, аналогичны свойствам функций одной переменной, непрерывных на отрезке (ограниченность функции, достижимость наибольшего и наименьшего значений и т.п.)
Частные производные, дифференцируемость, градиент функции многих переменных
Частные производные.
Частной производной функции 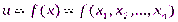 по переменной
по переменной 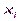 в точке
в точке
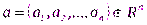 называют производную функции
называют производную функции 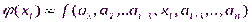
по переменной 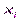 :
: 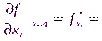
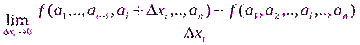 .
.
Дифференцируемость
Опр: Функция 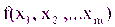 определенная в окрестности
определенная в окрестности 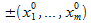 называется дифференцируемой в этой точке, если ее приращение Δf в
называется дифференцируемой в этой точке, если ее приращение Δf в 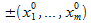 :
:
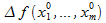 =
= 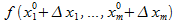 –
– 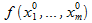 =
= 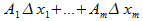 +
+ 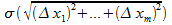 , что
, что 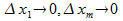
Необходимое условие дифференцируемости:
Если ф-ция 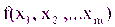 дифференцируема в
дифференцируема в 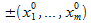 , то,
, то,
1.Она непрерывна в этой окрестности.
2.Существуют частные производные 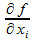 , i=1,...,m; причем
, i=1,...,m; причем 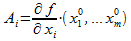
Док-во:
Если дифф.,то 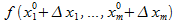 =
= 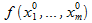 +
+ 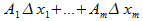 +
+ 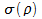 ,
,
lim 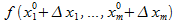
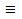 lim
lim 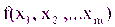 (при
(при 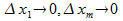 и
и 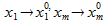 )=
)= 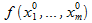
Следовательно, 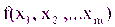 непрерывна в
непрерывна в 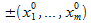 .
.
Докажем, что в 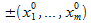 сущ.
сущ. 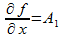
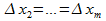 =0.
=0.
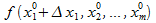 –
– 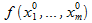 =
= 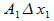 +
+ 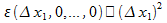 , НО lim
, НО lim 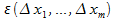 =0,
=0, 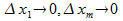 . Значит, lim
. Значит, lim 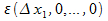 =0 (аналог предела по направлению для функции m переменных)
=0 (аналог предела по направлению для функции m переменных)
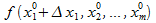 –
– 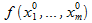 =
= 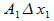 +
+ 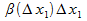 , где
, где 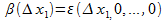
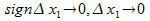 .
.
( 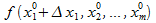 –
– 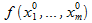 )/
)/ 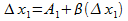
Тогда в пределе при 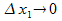 существует
существует 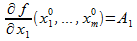 что и требовалось доказать.
что и требовалось доказать.
Определение. Градиентом функции многих переменных в данной точке называется вектор, координаты которого равны частным производным по соответствующим аргументам, вычисленным в данной точке.
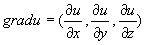 .
.
