Геометрическая интерпретация ЗЛП
Приведём геометрическую интерпретацию ЗЛП. Пусть дана ЗЛП от двух переменных:
c1x1+c2x2 ® max
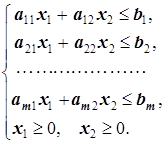 (3.1)
(3.1)
Из 3.1.1 и 3.1.2 получаем
3.2.1. Область допустимых решений ЗЛП (3.1) является выпуклым многоугольником (возможно, бесконечным) в R2 с конечным числом вершин.
3.2.2. Целевая функция ЗЛП (3.1) достигает экстремума в вершине многоугольника допустимых решений. При этом, если целевая функция достигает экстремума в двух вершинах многоугольника решений, то она также достигает экстремума на всей стороне (в любой точке стороны) с концами в этих вершинах.
Наконец, из 3.3.1 вводной Главы 0 получаем
3.3.2. При перемещении линий уровня c1x1+c2x2=a относительно начала координат в направлении вектора нормали 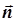 =(c1, c2) этих (прямых) линий значение a возрастает, в противоположном направлении a убывает.
=(c1, c2) этих (прямых) линий значение a возрастает, в противоположном направлении a убывает.
Действительно, при перемещении линий уровня c1x1+c2x2=a относительно начала координат в направлении вектора нормали 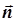 =(c1, c2) значения переменных x1, x2 целевой функции c1x1+c2x2 меняются пропорционально координатам вектора
=(c1, c2) значения переменных x1, x2 целевой функции c1x1+c2x2 меняются пропорционально координатам вектора 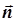 , скажем, с коэффициентом пропорциональности k. И если k растёт, то линии уровня перемещаются относительно начала координат по направлению вектора
, скажем, с коэффициентом пропорциональности k. И если k растёт, то линии уровня перемещаются относительно начала координат по направлению вектора 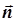 , а при убывании k линии уровня перемещаются относительно начала координат в противоположном с
, а при убывании k линии уровня перемещаются относительно начала координат в противоположном с 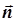 направлении. Поэтому в первом случае a растёт, во втором a убывает.
направлении. Поэтому в первом случае a растёт, во втором a убывает.
На фактах 3.2.1 - 3.2.3 основывается геометрический метод решения задачи (3.1), который заключается в следующем:
1. Построить область (многоугольник) допустимых решений ЗЛП (3.1).
2. Найти крайние положения прямых уровня c1x1+c2x2=a относительно ОДР. Эти положения будут либо в угловой точке (вершине), либо на стороне ОДР (многоугольника), либо таких точек не существует.
3. По направлению вектора нормали 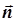 =(c1, c2) определить характер экстремума в найденных в пункте 2 точках.
=(c1, c2) определить характер экстремума в найденных в пункте 2 точках.
Пример. Решить геометрически ЗЛП:
4x1+x2 ® max
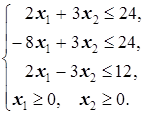
Решение. 1. Построим область допустимых решений задачи. Для этого построим полуплоскости, определяемые неравенствами системы ограничений. В свою очередь, для построения полуплоскости, определяемой неравенством a1x1+a2x2≤b, достаточно построить границу полуплоскости - прямую a1x1+a2x2=b, и определить, которая из двух полуплоскостей относитель 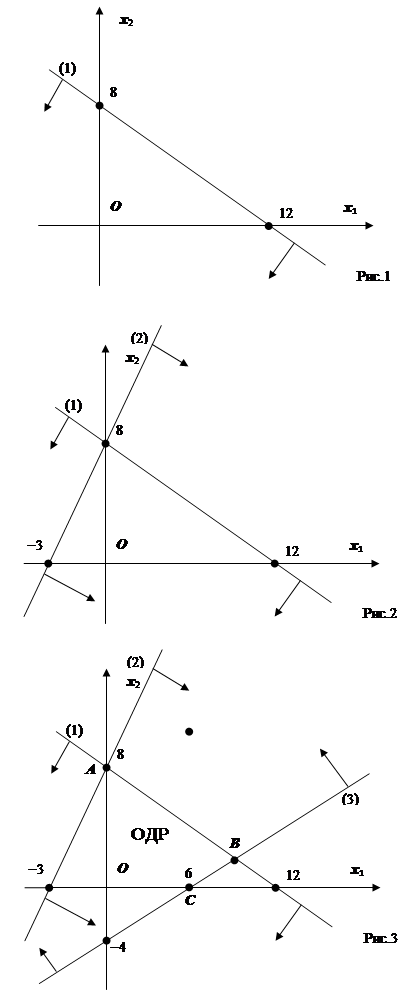 но этой прямой является искомой. Для этого подставляем координаты какой-нибудь точки, не лежащей на прямой a1x1+a2x2=b, в интересующее нас неравенство. Если получается верное числовое неравенство, то та сторона от прямой, в которой лежит точка, является искомой полуплоскостью.
но этой прямой является искомой. Для этого подставляем координаты какой-нибудь точки, не лежащей на прямой a1x1+a2x2=b, в интересующее нас неравенство. Если получается верное числовое неравенство, то та сторона от прямой, в которой лежит точка, является искомой полуплоскостью.
Построим полуплоскость 2x1+3x2≤24.
Прямая 2x1+3x2=24 пересекает оси Ox1 и Ox2 в точках (0, 8) и (12, 0). Подставим координаты начала координат в неравенство: 2×0+3×0≤24. Так как получилось верное неравенство, то начало координат лежит в искомой полуплоскости. Это означает, что та сторона относительно прямой, в которой лежит начало координат О, является полуплоскостью 2x1+3x2≤24. Цифрами в скобках нумеруем границы полуплоскостей в порядке их следования в системе ограничений (Рис.1).
Строим полуплоскость -8x1+3x2≤24.
Точки (0, 8), (-3, 0) - точки пересечения границы полуплоскости -8x1+3x2≤24 с осями координат. Далее, -8×0+3×0≤24 - верное числовое неравенство. Значит, искомая полуплоскость - та, в которой лежит начало координат (Рис. 2).
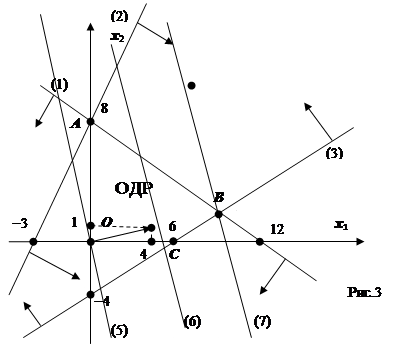
Наконец, (0, -4), (6, 0) - точки пересечения прямой 2x1-3x2≤12 с осями координат, 2×0-3×0≤12.
Четырёхугольник OABC - ОДР задач. (Рис. 3).
 2. Найдём крайние положения прямых уровня 4x1+x2=a относительно ОДР. Эти прямые перпендикулярны вектору
2. Найдём крайние положения прямых уровня 4x1+x2=a относительно ОДР. Эти прямые перпендикулярны вектору 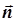 =(4, 1). Из них мы изобразили три: (5), (6), (7). Крайние положения достигаются в точках O и B. Причём прямая, проходящая через O, получается перемещением этих прямых против направления
=(4, 1). Из них мы изобразили три: (5), (6), (7). Крайние положения достигаются в точках O и B. Причём прямая, проходящая через O, получается перемещением этих прямых против направления 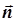 , а прямая, проходящая через B, получается перемещением этих прямых в направлении
, а прямая, проходящая через B, получается перемещением этих прямых в направлении 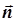 . Поэтому в точке O достигается минимум целевой функции f(x1, x2)=4x1+x2, а в B - максимум. Координаты B находим как координаты точки пересечения прямых (1) и (3), составив и решив систему из их уравнений:
. Поэтому в точке O достигается минимум целевой функции f(x1, x2)=4x1+x2, а в B - максимум. Координаты B находим как координаты точки пересечения прямых (1) и (3), составив и решив систему из их уравнений:
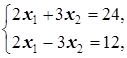 Û
Û 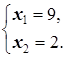
fmin=f(0, 0)=0, fmax=4×9+2=38.
Ответ: При x1=x2=0 достигается минимум целевой функции, равной 0; при x1=9, x1=2 достигается максимум, равный 38.
3.3. Упражнение. Задания 2) и 3) Упражнения 1.3 решить геометрическим методом.
