Абсолютная и относительная погрешности. Погрешности вычислительного алгоритма
Погрешности вычислительного алгоритма.
Необходимо подчеркнуть, что процесс исследования исходного объекта методом математического моделирования и вычислительного эксперимента неизбежно носит приближенный характер, потому что на каждом этапе вносятся те или иные погрешности. Так, построение математической модели связано с упрощением исходного явления, недостаточно точным заданием коэффициентов уравнения и других входных данных. По отношению к численному методу, реализующему данную математическую модель, указанные погрешности являются неустранимыми, поскольку они неизбежны в рамках данной модели.
При переходе от математической модели к численному методу возникают погрешности, называемые погрешностями метода. Они связаны с тем, что всякий численный метод воспроизводит исходную математическую модель приближенно. Наиболее типичными погрешностями метода являются погрешность дискретизации и погрешность округления. Поясним причины возникновения таких погрешностей.
Обычно построение численного метода для заданной математической модели разбивается на два этапа: а) формулировка дискретной задачи, б) разработка вычислительного алгоритма, позволяющего отыскать решение дискретной задачи. Например, если исходная математическая задача сформулирована в виде системы дифференциальных уравнений, то для численного решения необходимо заменить ее системой конечного, может быть, очень большого числа линейных или разностных алгебраических уравнений. В этом случае говорят, что проведена дискретизация исходной математической задачи. Простейшим примером дискретизации является построение разностной схемы путем замены дифференциальных выражений конечно-разностными отношениями. В общем случае дискретную модель можно рассматривать как конечномерный аналог исходной математической задачи. Ясно, что решение дискретизированной задачи отличается от решения исходной задачи. Разность соответствующих решений и называется погрешностью дискретизации.
Как уже отмечалось, дискретная модель представляет собой систему большого числа алгебраических уравнений. Невозможно найти решение такой системы точно и в явном виде. Поэтому приходится использовать тот или иной численный алгоритм решения системы алгебраических уравнений. Входные данные этой системы, а именно коэффициенты и правые части, задаются в ЭВМ не точно, а с округлением. В процессе работы алгоритма погрешности округления обычно накапливаются, и в результате решение, полученное на ЭВМ, будет отличаться от точного решения дискретизированной задачи. Результирующая погрешность называется погрешностью округления (иногда ее называют вычислительной погрешностью). Величина этой погрешности определяется двумя факторами: точностью представления вещественных чисел в ЭВМ и чувствительностью данного алгоритма к погрешностям округления.
Абсолютная и относительная погрешности
Пусть имеется некоторая числовая величина, и числовое значение, которое ей присвоено 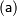 , считается точным, тогда под погрешностью приближенного значения числовой величины (ошибкой)
, считается точным, тогда под погрешностью приближенного значения числовой величины (ошибкой) 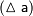 понимают разность между точным и приближенным значением числовой величины:
понимают разность между точным и приближенным значением числовой величины: 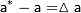
Погрешность может принимать как положительное так и отрицательное значение. Величина 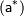 называется известным приближением к точному значению числовой величины - любое число, которое используется вместо точного значения. Простейшей количественной мерой ошибки является абсолютная погрешность.
называется известным приближением к точному значению числовой величины - любое число, которое используется вместо точного значения. Простейшей количественной мерой ошибки является абсолютная погрешность.
Абсолютной погрешностью приближенного значения 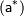 называют величину
называют величину 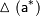 , про которую известно, что:
, про которую известно, что:
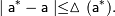
Качество приближения существенным образом зависит от принятых единиц измерения и масштабов величин, поэтому целесообразно соотнести погрешность величины и ее значение, для чего вводится понятие относительной погрешности.
Относительной погрешностью приближенного значения называют величину 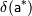 , про которую известно, что:
, про которую известно, что: 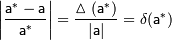
.
Относительную погрешность часто выражают в процентах. Использование относительных погрешностей удобно, в частности, тем, что они не зависят от масштабов величин и единиц измерения.
Так как точное значение обычно неизвестно, то непосредственное вычисление величин абсолютной и относительной погрешностей по предложенным формулам невозможно. Более реальная и часто поддающаяся решению задача состоит в получении оценок погрешности вида:
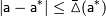
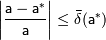 (*)
(*)
где 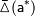 и
и 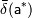 — известные величины, которые называют верхними границами (или просто границами) абсолютной и относительной погрешностей.
— известные величины, которые называют верхними границами (или просто границами) абсолютной и относительной погрешностей.
Поскольку точное значение  неизвестно, на практике используют приближенные равенства вида:
неизвестно, на практике используют приближенные равенства вида:
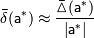
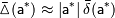
В литературе по методам вычислений широко используется термин "точность". Точное значение величины — это значение, не содержащее погрешности. Повышение точности воспринимается как уменьшение погрешности. Часто используемая фраза "требуется найти решение с заданной точностью  " означает, что ставится задача о нахождении приближенного решения, принятая мера погрешности которого не превышает заданной величины
" означает, что ставится задача о нахождении приближенного решения, принятая мера погрешности которого не превышает заданной величины  . Вообще говоря, следовало бы говорить об абсолютной точности и относительной точности, но часто этого не делают, считая, что из контекста ясно, как измеряется величина погрешности.
. Вообще говоря, следовало бы говорить об абсолютной точности и относительной точности, но часто этого не делают, считая, что из контекста ясно, как измеряется величина погрешности.
