Свободные незатухающие колебания.

Колебания– движения или состояния, параметры которых повторяются во времени. Колебания в той или иной мере встречаются во всех явлениях природы: от пульсации излучения звёзд, движения планет до внутриклеточных процессов или колебаний атомов и молекул, колебаний полей.

В физике особо выделяют механические и электромагнитные колебания (и их комбинации).

Моделью для изучения механических колебаний является осциллятор–материальная точка или система, совершающая колебательное периодическое движение около положения устойчивого равновесия.(Более того, термин осциллятор применим к любой системе, если описывающие её величины периодически меняются во времени.) Простейшие примеры осцилляторов – грузик на пружине, маятник.

П 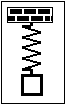ример.Груз массы m подвешен на невесомой пружине жесткости k в поле сил тяжести (пружинный маятник). Найти период его колебаний. Сопротивлением воздуха пренебречь.

Решение. Запишем уравнение его движения в проекции на вертикальное направлениеY:

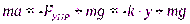или .

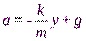где y– величина растяжения пружины. Положение равновесия груза на пружине: 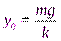. Введём смещение x груза от положения равновесия: 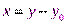, тогда , .

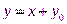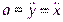Получаем уравнение: 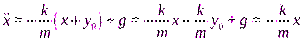, 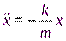. Перенесём в последнем соотношении все слагаемые в левую часть и вспомним, что дифференциальное уравнение, описывающее свободные незатухающие колебания, имеет вид: .

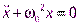Тогда у нас 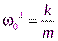и тогда период колебаний .

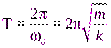Механическая энергия груза на пружине: .§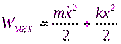

Пример.Найдем период колебаний математического маятника - материальной точки массы m, подвешенной на невесомой нерастяжимой нити длины l.

Р 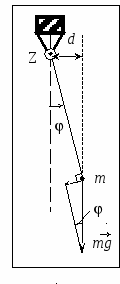ешение. Рассмотрим движение маятника в тот момент, когда он поднимается. Отклонение нити от вертикали зададим угловой координатойj. При этом, если уголjувеличивается (против часовой стрелки), то касательное ускорение точки направлено против направления движения. Поэтому уравнение движения имеет вид:

.

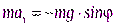Вблизи положения равновесия проекция силы тяжести должна быть представлена как квазиупругая сила. Если выполняется условие малости колебаний, то 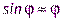, поэтому длина дуги окружности 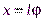, следовательно, проекция силы тяжести 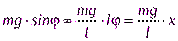. Поэтому коэффициент в выражении для квазиупругой силы 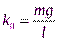. Касательное ускорение связано с угловым ускорением соотношением 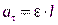(где 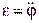), поэтому, после сокращения массыmполучим:

.

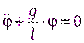С учетом выражения для циклической частоты 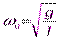период колебаний имеет вид: 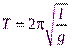. Механическая энергия математического маятника равна:

.

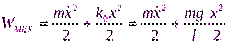При движении по окружности 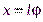, , 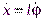поэтому

.
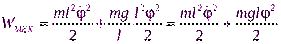