Основные понятия теории вероятности

Теория вероятности изучает следующую модель: опыт повторяется неограниченное количество раз. Любое множество исходов опыта называется событием. Говорят что в опыте наступило событие, если исход опыта принадлежит данному множеству.

Пример. Подбрасывают игральную кость – кубик, на гранях которого написаны цифры 1, 2, 3, 4, 5, 6. Событие «выпало чётное число очков» - это множество исходов { 2, 4, 6 }. Если выпало 6 очков, событие«выпало чётное число очков» наступило, если выпало 5 очков, оно не наступило.

Частотой события А называется отношение количества опытов, в результате которых событие А наступило, к общему количеству проведённых опытов. Предполагается, что с увеличением количества опытов частота события стремится к пределу, который называется вероятностью события, вероятность события А обозначается символом р ( А ).

Пример. Монету подбросили 40 раз, 17 раз выпал герб. Частота выпадения герба равна 17 / 40 или 0,425. Если монета идеальная (сделана из однородного материала и симметрична), то считается, что вероятность выпадения герба и вероятность выпадения решки равны ½, а вероятность того, что она станет на ребро равна нулю.

Частота и вероятность события являются безразмерными величинами, это означает, что они не изменяются при переходе к другой системе единиц измерения. Частота и вероятность события не могут быть меньше нуля или больше единицы. Событие, вероятность которого равна 1, происходит при любом (почти при любом) исходе опыта, событие, вероятность которого равна 0, никогда (почти никогда) не наступает.

Вероятность того, что в результате опыта наступит хотя бы одно из событий А, В вычисляется по формуле:

р ( А или В ) = р ( А ) + р ( В ) - р ( А и В ),

где р ( А и В ) - вероятность того, что в опыте наступят оба события А и В.

События А, В называются несовместными, если они не могут наступить в одном опыте, для несовместных событий р ( А и В ) = 0. Событие A и событие «не A» (событие A не наступило) несовместны, вероятность того, что наступит событие ( A или не A ) равна 1, следовательно, p ( не A ) = 1 – p ( A )

Величина, значение которой определяется исходом опыта, называется случайной величиной.

Пример. Число очков, которое выпадает при бросании игральной кости, является случайной величиной, эта случайная величина может принимать значения 1, 2, 3, 4, 5, 6.

Предел, к которому стремится среднее значение случайной величины Х, вычисленное по результатам n опытов, когда n неограниченно возрастает, называется математическим ожиданием случайной величины Х и обозначается символом МХ. Математическое ожидание суммы случайных величин равна сумме их математических ожиданий: для любых случайных величин X, Y M ( X + Y ) = MX + MY. Постоянный множитель можно выносить за знак математического ожидания: M ( a X ) = a M ( X ).

Среднее значение случайной величины и ее математическое ожидание измеряется в тех же единицах, что и сама случайная величина.

Если идеальная игральная кость бросают n раз, то каждое число очков выпадет примерно n / 6 раз, так что среднее число выпавших очков будет приблизительно равно

( 1· n / 6 + 2 · n / 6 + 3 · n / 6 +

4 · n / 6 + 5 · n / 6 + 6 · n / 6 ) / n =

( 1 + 2 + 3 + 4 + 5 + 6 ) / 6 = 3,5

Таким образом, математическое ожидание числа выпавших очков равно 3,5.

Случайная величина X называется дискретной, если все её значения можно представить в виде (конечной или бесконечной) последовательности x₁, x₂ ,.... Математическое ожидание дискретной случайной величины вычисляется по формуле:

M ( X ) = x₁ p ( X = x₁) + x₂ p ( X = x₂ ) +...,

где p ( X = x_k ) - вероятность того, что в результате опыта значение случайной величины X будет равно x_k.

Пример. Количество выпадений герба при бросании монеты является случайной величиной, которое с вероятностью ½ может принимать значения 0 и 1. Математическое ожидание этой величины равно

0 · ½ + 1 · ½ = ½.

Пусть g – числовая функция, X- дискретная случайная величина. Случайная величина g ( X ) также будет дискретной, её математическое ожидание можно найти так:

M g ( X ) = g ( x₁ ) p ( X = x₁) + g ( x₂) p ( X = x₂ ) +...,

Дисперсией случайной величины Х называется математическое ожидание квадрата разности между случайной величиной и её математическим ожиданием:

DХ = М ( | X - MX |² ).

Дисперсия случайной величины неотрицательна, для любой случайной величины X и любого числа a

D ( a X ) = a² DX.

Квадратный корень из дисперсии называется квадратичным или стандартным отклонением случайной величины Х. Квадратичное отклонение выражается в тех же единицах измерения, что и сама случайная величина Х, она характеризует разброс значений величины Х вокруг ее математического ожидания.

Иногда удобно считать, что постоянная величина a является вырожденной случайной величиной, принимающей при любом исходе опыта одно и то же значение a. Математическое ожидание такой величины равно a, а её дисперсия нулевая.

Обычно формулу для вычисления дисперсии преобразуют:

DХ = М ( | X - MX |² ) = M ( X X – 2 ( MX) X + ( MX ) ( MX )) = M ( X X ) - 2 ( MX ) MX + ( MX ) ( MX ) = M ( X²) - ( MX )² ;

Таким образом, дисперсия случайной величины X равна

M ( X²) - ( MX )².

Задание. Определите дисперсию количества очков, выпадающих при бросании игральной кости и дисперсию количества гербов, выпадающих при бросании монеты.

Функцией распределения случайной величины X называется числовая функция F_X ( s ), которая определяется следующим образом: F_X ( s ) = p ( X < s ) для любого вещественного значения аргумента s.

Пример. Если X – количество гербов, выпавших при бросании монеты, то

F_X ( s ) = 0, когда s ≤ 0, F_X ( s ) = ½, когда 0 < s ≤ 1 и F_X ( s ) = 1, когда s > 1.

Задание. Определите функцию распределения количества очков, выпавших при бросании игральной кости.

В моделировании случайных величин используется случайная величина, равномерно распределённая на интервале ] 0, 1 [. Будем обозначать её буквой E. Она имеет следующую функцию распределения:

F_E ( s ) = 0, когда s≤ 0, F_E ( s ) = s, когда 0 < s < 1 и F_E ( s ) = 1, когда s ≥ 1.

Случайная величина X называется непрерывной, если её функцию распределения можно представить в виде интеграла:

F_X ( s ) = 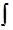[ -∞, s ] f_X ( u ) du

для всех s. Функция f_X называется в этом случае плотностью случайной величины X. Плотность случайной величины E равна 1 в точках интервала ] 0, 1 [ и равна нулю во всех остальных точках числовой прямой.

Математическое ожидание непрерывной случайной величины X с плотностью f_X вычисляют по формуле

M ( X ) = 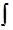[ -∞, +∞, ] s f_X ( s ) dt .

Аналогичная формула справедлива для случайной величины g ( X ), где g ̶ числовая функция:

M ( g ( X )) = 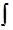[ -∞, +∞ ] g ( s ) f_X ( s ) ds

(в левой части равенства аргументом функции g служит случайная величина X, g ( X ) ̶ случайная величина; в правой части равенства аргументом функции g служит число s, g ( s ) ̶ значение числовой функции).

В частности,

D ( X ) = M ( | X – MX |² ) = 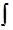[ -∞, +∞ ] | s – MX |² f_X ( s ) ds;

M ( X²)) = 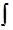[ -∞, +∞ ] s² f_X ( s ) ds.

Напомним, что

D ( X ) = M ( X² ) - ( MX )²

Задание. Нарисуйте график функции распределения случайной величины E, равномерно распределённой на интервале ] 0, 1 [ и её плотности, вычислите её математическое ожидание и дисперсию.

Пусть X = α E + β, где E – случайная величина, равномерно распределённая на интервале ] 0, 1 [, α, β – вещественные числа, α > 0. Для любого вещественного числа s следующие утверждения эквивалентны:

X < s, α E + β < s, E < ( s - β ) / α,

следовательно, F_X ( s ) = F_E ( ( s - β ) / α ). Случайная величина α E + β равномерно распределена на интервале ] β, α + β [.

Задание. Определите функцию распределения, плотность, математическое ожидание и дисперсию случайной величины, равномерно распределённой на интервале ] a, b [, нарисуйте графики её функции распределения и плотности.

Говорят, что случайная величина N имеет нормальное распределение (является нормальной случайной величиной, распределена по нормальному закону), если её плотность определяется следующим образом:

f_N ( s ) = exp ( - ( s - m )² / ( 2 σ²)) / ( σ ( 2 π )^½).

Числа m и σ называются параметрами нормальной случайной величины, m равно её математическому ожиданию, σ – её квадратичному отклонению.

Задание. Найдите математическое ожидание, дисперсию, квадратичное отклонение нормально распределённой случайной величины с параметрами m, σ.

Если случайная величина N распределена по нормальному закону с параметрами m, σ, то величина ( N – m ) / σ является нормальной случайной величиной с параметрами ( 0, 1 ).

Задание. Докажите, что случайная величина N распределена по нормальному закону с параметрами m, σ тогда и только тогда, когда величина ( N – m ) / σ является нормальной случайной величиной с параметрами ( 0, 1 ).

Случайные величины X₁, X₂,..., X_n называются взаимно независимыми, если для любых числовых множеств A₁, A₂,..., A_n вероятность того, что в результате опыта значение величины X₁ будет принадлежать множеству A₁, значение величины X₂ будет принадлежать множеству A₂, ... значение величины X_n будет принадлежать множеству A_n , равно произведению вероятностей этих событий:

p ( значение величины X₁ принадлежит множеству A₁, и значение величины X₂ принадлежит множеству A₂, и ... и значение величины X_n принадлежит множеству A_n ) = p ( значение величины X₁ принадлежит множеству A₁ ) p ( значение величины X₂ принадлежит множеству A₂ )... p ( значение величины X_n принадлежит множеству A_n ).

Центральная предельная теорема. Пусть взаимно независимые случайные величины X₁, X₂,..., X_n обладают одной и той же функцией распределения, математическим ожиданием m и дисперсией d. Если число n достаточно велико, то их среднее арифметическое ( X₁+ X₂ +...+ X_n ) / n можно считать нормальной случайной величиной с математическим ожиданием m и дисперсией d / n.

Таким образом, нормальными являются те случайные величины, значения которых определяются влиянием большого количества незначительных факторов, действующих независимо друг от друга.