Примеры решения типовых задач. 1. Написать уравнение плоскости, проходящей через точку М(-1;1,3) перпендикулярно вектору .

1. Написать уравнение плоскости, проходящей через точку М(-1;1,3) перпендикулярно вектору .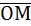

Решение:

Найдем координаты вектора 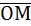: О(0;0;0); М(-1;1;3) Þ

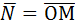{-1;1;3}.

Уравнение плоскости имеет вид:

A(x-x₀)+B(y-y₀)+C(z-z₀)=0

А=-1, В=1, С=3 – координаты вектора нормали.

X₀=-1, y₀=1, z₀=3.

-1(х+1)+1(у-1)+3(z-3)=0

-х-1+у-1+3z-9=0

-х+у+3z-11=0.

Ответ: -х+у+3z-11=0.

2.Написать уравнение плоскости, проходящей через точки М₁(1;-1;3), М₂(2;-1;0), М₃(4;2;-1).

Решение:

Уравнение плоскости, проходящей через три точки имеет вид:

,

,

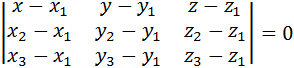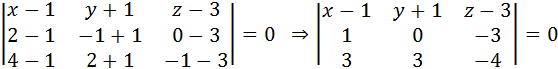
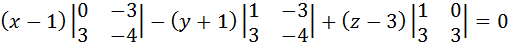9(х-1)-5(у+1)+3(z-3)=0

9х-9-5у-5+3z-9=0

9х-5у+3z-23=0.

Ответ: 9х-5у+3z-23=0.

3. Написать уравнение плоскости, проходящей через точку М₀(-2;7;3) параллельно плоскости х-4у+5z+1=0 (рис.10).

{1;-4;5}

y ZXYueG1sTI/BTsMwEETvSPyDtUhcqtYhqG6bZlOhSlzgABQ+wIndJMJeh9hN3b/HPcFxNKOZN+Uu WsMmPfreEcLDIgOmqXGqpxbh6/N5vgbmgyQljSONcNEedtXtTSkL5c70oadDaFkqIV9IhC6EoeDc N5220i/coCl5RzdaGZIcW65GeU7l1vA8ywS3sqe00MlB7zvdfB9OFuHl7X12yaOY/ayW9T5OaxNf vUG8v4tPW2BBx/AXhit+QocqMdXuRMozgyA2eUoizFfArrZ4TNdqhOVGAK9K/p+/+gUAAP//AwBQ SwECLQAUAAYACAAAACEAtoM4kv4AAADhAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlw ZXNdLnhtbFBLAQItABQABgAIAAAAIQA4/SH/1gAAAJQBAAALAAAAAAAAAAAAAAAAAC8BAABfcmVs cy8ucmVsc1BLAQItABQABgAIAAAAIQAxJKdT8wEAAOsDAAAOAAAAAAAAAAAAAAAAAC4CAABkcnMv ZTJvRG9jLnhtbFBLAQItABQABgAIAAAAIQBhKIaV3QAAAAcBAAAPAAAAAAAAAAAAAAAAAE0EAABk cnMvZG93bnJldi54bWxQSwUGAAAAAAQABADzAAAAVwUAAAAA " strokecolor="black [3040]"/>

М0(-2;7;3)

Рис. 10

Решение:

Нормальный вектор для плоскости х-4у+5z+1=0 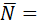{1;-4;5} является нормальным для искомой плоскости. Так как плоскость проходит через точку М₀(-2;7;3), то уравнение плоскости имеет вид:

A(x-x₀)+B(y-y₀)+C(z-z₀)=0;

1(х+2)-4(у-7)+5(z-3)=0;

х+2-4у+28+5z-15=0;

х-4у+5z+15=0.

Ответ: х-4у+5z+15=0.

4. Найти расстояние от точки М₀(1;-1;3) до плоскости 13х+2у- -5z+1=0.

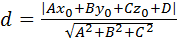; х₀=1; у₀=-1; z₀=3.

А=13; В=2; С=-5, D=1.

.

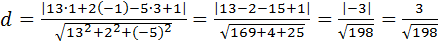Ответ: d= .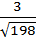

5. Найти угол между плоскостями х+у-1=0 и 2х-у+3z-1=0.

Решение:

Угол между плоскостями определяем как угол между нормалями к этим плоскостям. Из общих уравнений плоскостей определяем координаты нормалей 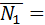{1;1;0}, 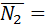{2;-1;3}.

.

.

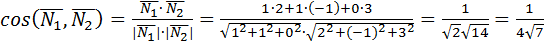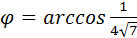Ответ: .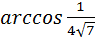

Прямая в пространстве.

Прямая и плоскость

Различным способам задания прямой в пространстве соответствуют разные виды ее уравнений, основные из которых представлены в табл. 4.

Таблица 4

№ п/п	Вид уравнения	Смысл входящих в уравнение коэффициентов	Примечание
	Канонические уравнения прямой	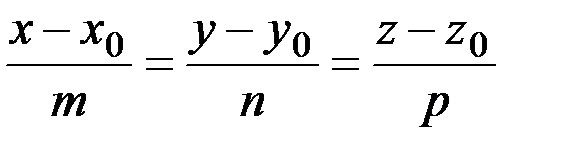(x0,y0,z0) – координаты точки М0, лежащей на прямой; m,n,p – координаты вектора, параллельного прямой	Вектор 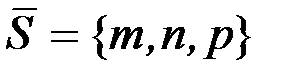называется направля-ющим вектором прямой
	Уравнение прямой, проходящей через две заданные точки	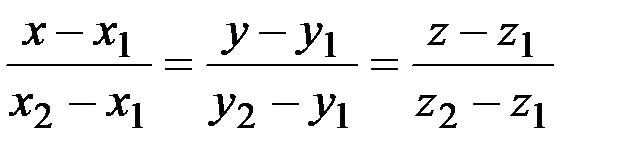(x1,y1,z1), (x2,y2,z2) – координаты двух заданных точек	Уравнение является обобще-нием уравнения прямой на плоскости
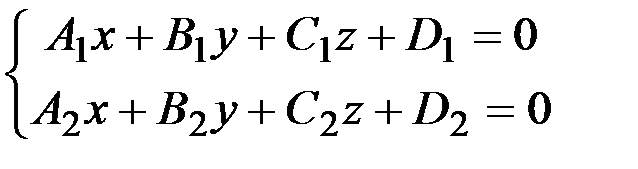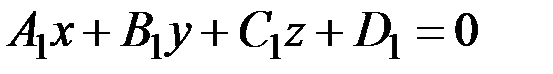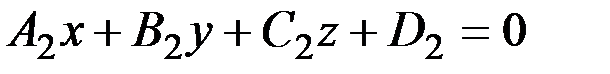	Уравнения прямой как линии пересечения двух плоскостей	- уравнение одной плоскости; - уравнение второй плоскости	Уравнения иначе назы-ваются общими уравне-ниями прямой в простран-стве

Пусть заданы две прямые своими каноническими уравнениями:

l₁: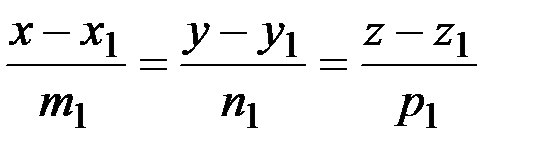

l₂: .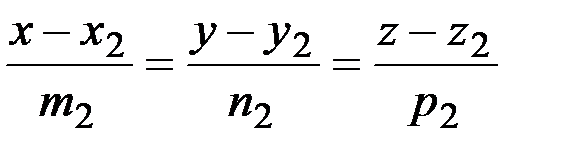

Угол между прямыми определяется как .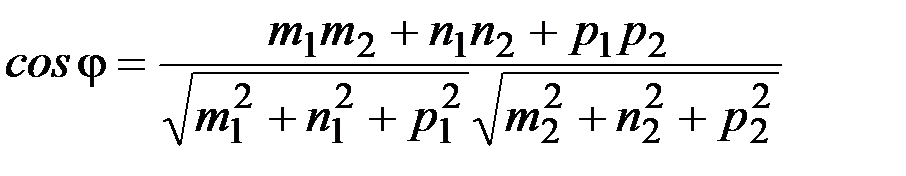

Условие перпендикулярности прямых:

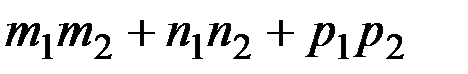=0.

Условие параллельности прямых:

.

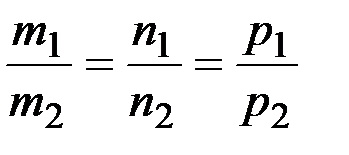Пусть плоскость a задана уравнением Ах+Ву+Сz+D=0, а прямая l – своими каноническими уравнениями 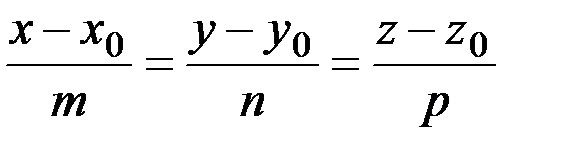, тогда угол между прямой и плоскостью определяется как

.

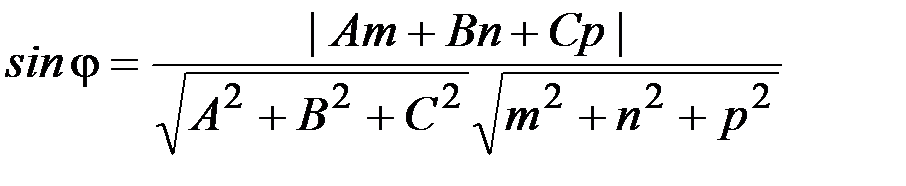Условие параллельности прямой и плоскости Аm+Bn+Cp=0.

Условие перпендикулярности прямой и плоскости:

.
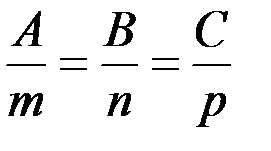