Часть 1. Дайте краткий ответ.

Вариант 2.

Часть 1. Дайте краткий ответ.

1. Вычислите предел .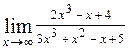

2. Найдите производную сложной функции .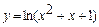

3. Найдите полный дифференциал функции .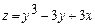

4. Проинтегрируйте функцию способом подстановки .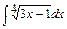

5. Решите дифференциальное уравнение с постоянными коэффициентами .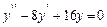

6. Исследуйте ряд на сходимость, используя признак Коши .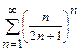

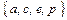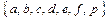7. Даны множества А = , В = . Найдите А 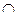В.

8. В урне находятся 7белых, 3 чёрных и 5 красных шаров. Достали 1 шар. Какова вероятность того, что он чёрный?

9. По заданному закону распределения случайной величины Х найти её математическое ожидание.

Х
р	0,4	0,1	0,2	0,1	0,2

10 Выполните действия 2А – 5В, если А = 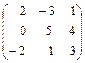, В = .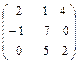

11 Решите данную систему по формулам Крамера: .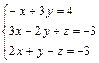

12 Определите взаимное расположение прямых .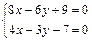

13 Составьте математическую модель задачи:

С помощью трех технологических способов выпускается два вида продукции. При использовании первого технологического способа в течение всего рассматриваемого периода выпускается одновременно 9 единиц продукции первого вида и 16 – второго. При использовании второго способа выпускается 12 единиц продукции первого вида и 20 – второго и при использовании третьего способа выпускается 15 единиц продукции первого вида и 15 – второго. Затраты для каждого из них составляют 20, 12 и 8 ч – дней. Прибыль от реализации единицы продукции первого вида составляет 1000 руб, второго вида – 1500 руб. Составьте план производства продукции обоих видов, при котором прибыль от их реализации максимальна.

Часть 2. Запишите решение с полным его обоснованием.

1 Вычислите приближённо определённый интеграл по формуле трапеций 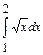, п = 5.

2 Составьте таблицу конечных разностей и запишите интерполяционный многочлен.

x
y

ИЛИ

Часть 1. Дайте краткий ответ.

1. Вычислите предел .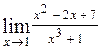

2. Найдите производную сложной функции .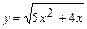

3. Найдите полный дифференциал функции .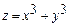

4. Проинтегрируйте функцию способом подстановки .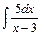

5. Решите дифференциальное уравнение с постоянными коэффициентами .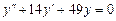

6. Исследуйте ряд на сходимость, применяя признак Даламбера .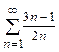

7. Даны множества А = 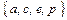, С = 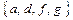. Найдите А С.

8. В урне находятся 4 белых и 7 чёрных шаров. Достали 1 шар. Какова вероятность того, что он белый?

9. По заданному закону распределения случайной величины Х найти её дисперсию.

Х
Р	0,4	0,1	0,3	0,1	0,1

10 Выполните действия 3А + 4В, если А = 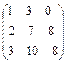, В = .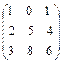

11 Решите данную систему по формулам Крамера: .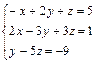

12 Определите взаимное расположение прямых .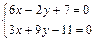

13 Составьте математическую модель задачи:

Для изготовления изделий А и В предприятие использует три вида сырья. На производство единицы изделия А требуется затратить сырья 1-го вида 11 кг, 2-го вида 8 кг, 3-го вида 5 кг. На производство единицы изделия В соответственно 3, 4, 3 кг. Производство обеспечено сырьём 1-го вида – 671 кг, 2-го вида – 588 кг, 3-го вида – 423 кг. Прибыль от реализации изделия А составляет 5 тыс. рублей, от изделия В – 2 тыс. рублей. Составьте план производства изделий А и В, при котором прибыль от их реализации максимальна.