Практический блок. Практические занятия.

№ темы   Тема1.2. Тема 1.3.	Наименование практических занятий	Кол-во часов по
дневной форме обуч. (56 часов)	очно-заочной форме. (36 часов)	заочной форме обуч. (20часов)
Решение систем линейных уравнений
Матрицы и их применение к решению систем
Тема 3.3.	Уравнения плоскости и прямой в пространстве
Тема 3.4.	Кривые второго порядка
Тема 3.5.	Поверхности второго порядка
Тема 4.3.	Способы вычисления пределов
Тема 4.4.	Непрерывность функции. Точки разрыва
Тема 4.5,	Производная функции
Тема 5.1.	Правило Лопиталя
Тема 5.2.	Применение производной для исследования функции
'Тема 7.1.	Первообразная. Неопределенный интефал
Тема 7.3.	Определённый интеграл. 11риложения
Тема 7.4.	Несобственный интеграл
'Тема 8.1.	Функции нескольких переменных
Тема 8.2.	Экстремумы функций нескольких переменных.

Блок контроля освоения дисциплины

Методические указания по выполнению контрольной работы №1

4.1.1. Определители и системы линейных уравнений[1],Гл.1,§6

В различных разделах курса высшей математики используется понятие определителя. Определителем второго порядка называется число, обозначаемое символом, 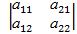и вычисляется по правилу:

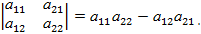
Например,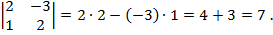

Определитель третьего порядка будем вычислять, раскладывая его по элементам какой-либо строки или какого-либо столбца:

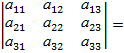
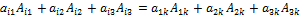
где I и к - целые числа от 1 до 3.

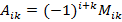- алгебраические дополнения элементов 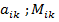- миноры элементов 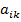- определители второго порядка, получаемые вычеркиванием строки и столбца, на пересечении которых расположен элемент .

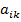Пример 1.

1) Вычислить определитель 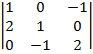, разложив его по элементам первой строки.

Решение:

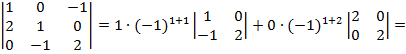
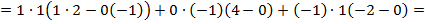
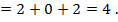
2) Вычислить определитель 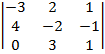, разложив его по элементам первого столбца.

Решение:

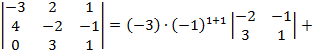
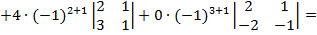
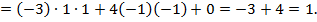
При решении систем п линейных уравнений с п неизвестными следует знать, что система имеет единственное решение в том и только в том случае, когда се определитель нс равен нулю. Решение системы уравнений в этом случае находят по формулам Крамера. Если же определитель системы равен нулю, система или несовместна, или имеет бесконечно много решений.

Пример 2. Решить систему уравнений

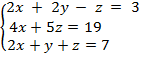
Решение: Вычисляем определитель системы - определитель, составленный из коэффициентов при неизвестных, разложив его, например, по элементам второго столбца.

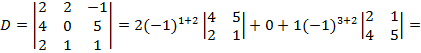
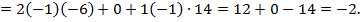
Так как D ≠ 0, то система имеет единственное решение, определяемое по формулам Крамера:

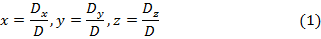
Здесь D – определитель системы, D_x , D_y , D_z ,– определители, получающиеся из определителя системы заменой столбца коэффициентов при соответствующем неизвестном столбцом свободных членов.

Вычисляем D_x , D_y , D_{z .}

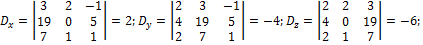
Таким образом,

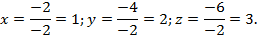
Проверяем полученное решение подставив значение x=1, y=2, z =3в систему уравнений

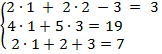
Все уравнения системы обратились в тождества, значит, система решена верно.