Пример решения задачи целочисленного программирования методом ветвей и границ
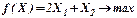 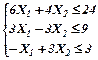 Хj≥0 (целые) Хj≥0 (целые) | 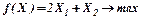 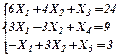 |
Решение исходной задачи линейного программирования без учета целочисленности
Х(I)=( 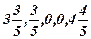 );f(X)=
);f(X)= 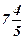 .
.
Для переменной Х1 = 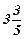 составим дополнительные ограничения для двух следующих задач:
составим дополнительные ограничения для двух следующих задач:
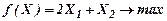 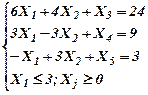 | 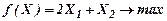 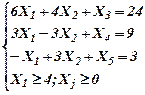 |
Х(А,I)=( 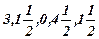 );f(X)=
);f(X)= 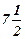 . Для задачи В.1 нет решения.
. Для задачи В.1 нет решения.
Для переменной Х2 = 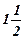 задачи А.1 составим дополнительные ограничения для следующей пары задач:
задачи А.1 составим дополнительные ограничения для следующей пары задач:
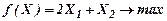 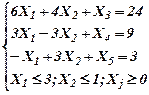 | 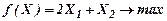 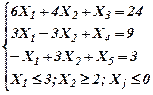 |
Х(А,2)=( 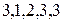 ); f(X)=
); f(X)= 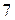 . Для задачи В.2 нет решения.
. Для задачи В.2 нет решения.
Задача
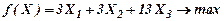
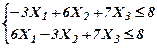
Хj ≥ 0 (целые)
В ходе решения получим f(X)=16, X = ( 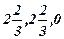 ) ;
) ;
0 ≤ Xj ≤ 5 (j = 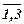 )
)
| А.1 3 ≤ X1 ≤ 5 0 ≤ X2 ≤ 5 0 ≤ X3 ≤ 5 | B.1 0 ≤ X1 ≤ 2 0 ≤ X2 ≤ 5 0 ≤ X3 ≤ 5 |
Для переменной Х1= 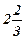 составим дополнительных ограничения для двух задач линейного программирования:
составим дополнительных ограничения для двух задач линейного программирования:
задача А.1 не имеет решения.
f(X) = 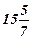 ; X=(
; X=( 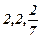 )
)
Для задачи В.1 для переменной Х3 = 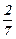 вводим дополнительные ограничения для двух новых задач линейного программирования:
вводим дополнительные ограничения для двух новых задач линейного программирования:
| А.2 0 ≤ X1 ≤ 2 0 ≤ X2 ≤ 5 1 ≤ X3 ≤ 5 | B.2 0 ≤ X1 ≤ 2 0 ≤ X2 ≤ 5 0 ≤ X3 ≤ 1 |
f(X)А.2=15; X=( 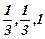 ) f(X)В.2=13; X=(
) f(X)В.2=13; X=( 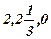 )
)
так как f(Х)А,2> f(Х)В,2, то для задачи А.2 для переменной Х2 = 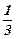 составим два дополнительных ограничения для двух новых задач линейного программирования:
составим два дополнительных ограничения для двух новых задач линейного программирования:
| А.3 0 ≤ X1 ≤ 2 1 ≤ X2 ≤ 5 1 ≤ X3 ≤ 5 | B.3 0 ≤ X1 ≤ 2 0 ≤ X2 ≤ 0 (Х2=0) 1 ≤ X3 ≤ 5 |
задача А.3 не имеет решения. f(X)В.3= 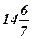 ; X=(
; X=( 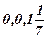 )
)
Для переменной Х3= 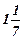 задачи В.3 составим два дополнительных ограничения для двух новых задач линейного программирования,
задачи В.3 составим два дополнительных ограничения для двух новых задач линейного программирования,
| А.4 0 ≤ X1 ≤ 2 0 ≤ X2 ≤ 0 (Х2=0) 2 ≤ X3 ≤ 5 | B.4 0 ≤ X1 ≤ 2 0 ≤ X2 ≤ 0 (Х2=0) 1 ≤ X3 ≤ 1 (Х1=1) |
задача А.4 не имеет решения. f(X)В.4=13; X=(0,0,1)
Значение целевых функций в задачах В.2 и В.4 равны между собой f(X)=13, но задача В.4 имеет целочисленное решение. Это окончательное решение.
Задача коммивояжера
Коммивояжер (агент по сбыту) собирается посетить каждые из n городов по одному разу, выехав из города 1 и вернувшись в него же. Расстояние между городом i и городом j равно Cij. Каков кратчайший маршрут коммивояжера?
Эта оптимизационная задача и различные ее модификации на самом деле возникают перед различными фирмами и агентствами, занимающимися доставкой товаров на дом и аналогичной деятельностью. Математическая модель этой задачи отображает также ситуации совершенно другого характера. Применение этой модели можно использовать для решения задач календарного планирования производства. Так, например, эта модель описывает условия производства продукции, когда нужно найти оптимальный порядок изготовления различных сортов на одном и том же оборудовании. Примем, что Cij представляет собой затраты времени на очистку и подготовку оборудования, когда сорт j изготовляется после сорта i. Величины Cij могут изменяться в широком диапазоне, ибо сорта, мало отличающиеся друг от друга, можно выпускать друг за другом, лишь незначительно изменив технологию, т.е. затратив немного времени на переналадку оборудования, тогда как для последовательного выпуска некоторых других сортов требуются значительные затраты времени на переналадку оборудования. Разумеется, стремятся составить такой календарный план выпуска различных сортов продукции, чтобы минимизировать затраты времени на переналадку оборудования. Возвращаясь к исходной задаче, примем
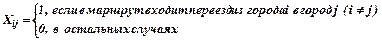
Предположим теперь, что для решения этой задачи применяется модель назначений, в которой применяется модель назначений, в которой исключены все Xii и отыскивается маршрут минимальной длины, проходящий через все города.
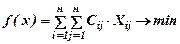 при ограничениях
при ограничениях
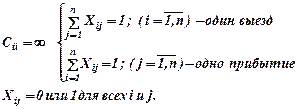
Ограничения задачи о назначениях обеспечивают включение в этот маршрут въезд из каждого города, а также прибытие в каждый город.
Можно ли получить при решении этой оптимизационной задачи маршрут, которым может воспользоваться коммивояжер? К сожалению, оптимальное решение задачи может не содержать такого маршрута. Полученное решение может включать два или более несвязанных цикла. Так, например, не исключается возможность такого решения:
Х12=Х23=Х31=1 и Х45=Х56=…..=Хn4=1.
Следовательно, один маршрут проходит через города 1,2 и 3 и совершенно независимый маршрут – через города 4,5,….., n. Поэтому кажущееся весьма скромным дополнительное требование о том, чтобы маршрут содержал только 1 цикл, на самом деле существенно усложняет решение этой комбинаторной задачи.
Задача коммивояжера.
| Переезд из города | в город | ||||
| ∞ | |||||
| ∞ | |||||
| ∞ | |||||
| ∞ | |||||
| ∞ |
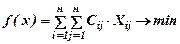
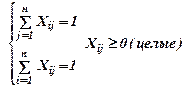
Решение
Х15=Х51=Х23=Х34=Х42=1. f(x)=60
 |  | ||
Получается 2 подрешения.
Используя метод ветвей и границ, решим 2 следующие задачи, положив
в одной С15= ∞, в другой С51= ∞
Получаем цикл длиной в f(x)=65; f(x)=62
Х12=Х23=Х34=Х45=Х51=1 Х15=Х52=Х23=Х34=Х41=1
(10 +10 + 20 +15 + 10 ) (10 + 8 +10 + 20 + 14 )
