Как выглядят эпюры касательных напряжений для балок прямоугольного и двутаврового поперечных сечений?
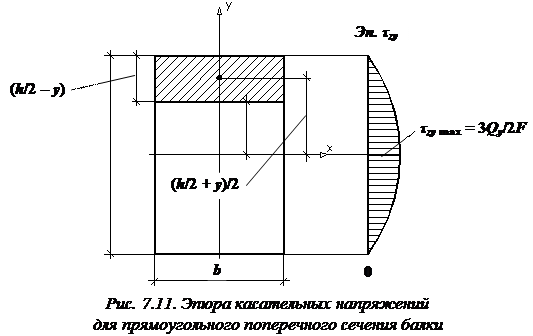
Напомним, что при выводе формулы Журавского мы предполагали, что балка имеет прямоугольное поперечное сечение (рис. 7.11), поэтому
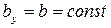 ;
; 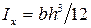 ;
; 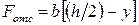 ;
; 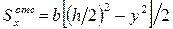 , (7.9)
, (7.9)
где y – расстояние от точки, в которой определяется касательное напряжение, до нейтральной оси x.
Подставляя выражения (7.9) в формулу (7.8), получим:
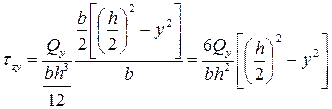 .
.
Отсюда видно, что для балки прямоугольного профиля касательные напряжения изменяются по высоте поперечного сечения по закону квадратичной параболы (см. рис. 7.11).
При 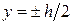 , то есть для точек, наиболее удаленных от нейтральной оси,
, то есть для точек, наиболее удаленных от нейтральной оси, 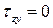 . Для точек, расположенных на нейтральной оси (при
. Для точек, расположенных на нейтральной оси (при 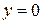 ), касательные напряжения достигают максимального значения:
), касательные напряжения достигают максимального значения:


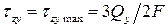 .
.
Характерной особенностью двутаврового сечения балки является то обстоятельство, что в том месте, где полка соединяется со стенкой, происходит резкое изменение ширины поперечного сечения 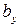 (рис. 7.12).
(рис. 7.12).
Определим касательное напряжение в некоторой точке K.
Для этого проведем через эту точку сечение. Ширина этого сечения равна толщине стенки, то есть 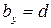 . Рассмотрим верхнюю отсеченную часть площади поперечного сечения, которая состоит из площади полки
. Рассмотрим верхнюю отсеченную часть площади поперечного сечения, которая состоит из площади полки 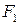 и площади части стенки
и площади части стенки 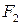 (обе эти площади на рис. 7.12, а заштрихованы). Статический момент этой отсеченной части площади поперечного сечения относительно нейтральной оси x равен:
(обе эти площади на рис. 7.12, а заштрихованы). Статический момент этой отсеченной части площади поперечного сечения относительно нейтральной оси x равен:
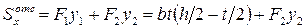 .
.






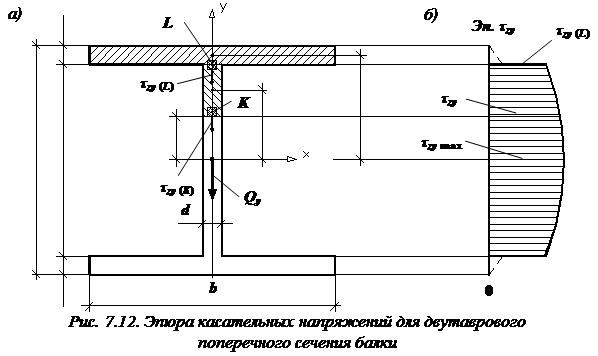
Эпюра касательных напряжений, возникающих в точках стенки двутавра, имеет вид, показанный на рис. 7.12, б.
Касательные напряжения 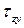 , возникающие в точках полки двутавра, по формуле Журавского вычислять нельзя, поскольку при ее выводе использовалось допущение о равномерности распределения касательных напряжений по ширине поперечного сечения, что справедливо только в том случае, если ширина сечения
, возникающие в точках полки двутавра, по формуле Журавского вычислять нельзя, поскольку при ее выводе использовалось допущение о равномерности распределения касательных напряжений по ширине поперечного сечения, что справедливо только в том случае, если ширина сечения 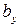 невелика. Однако очевидно, что эти напряжения малы и не оказывают практического влияния на прочность балки. Их эпюра показана штриховой линией (см. рис. 7.12, б).
невелика. Однако очевидно, что эти напряжения малы и не оказывают практического влияния на прочность балки. Их эпюра показана штриховой линией (см. рис. 7.12, б).
Касательное напряжение в точке L, то есть в том месте, где полка соединяется со стенкой, вычисляется по формуле
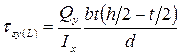 .
.
Как и для балки прямоугольного поперечного сечения, наибольшие касательные напряжения в балке двутаврового профиля возникают в точках, лежащих на нейтральной оси x.
7.30. И все-таки, по какой формуле можно вычислить значения касательных напряжений для балки прямоугольного поперечного сечения, если оно не является узким?
Точное решение задачи, полученное Сен-Венаном, показывает, что касательные напряжения при поперечном изгибе балки не одинаковы по ширине поперечного сечения. Наибольшие касательные напряжения возникают в точках, расположенных по краям нейтральной оси. Значения этих напряжений можно определить по следующей формуле
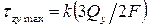 ,
,
где k – коэффициент, зависящий от отношения сторон 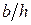 .
.
Так, например, при 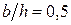 коэффициент
коэффициент 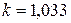 , то есть для узкого поперечного сечения формула Журавского дает практически точное значение. Если же сечение широкое, например,
, то есть для узкого поперечного сечения формула Журавского дает практически точное значение. Если же сечение широкое, например, 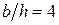 , то тогда коэффициент
, то тогда коэффициент 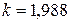 . Следовательно, формула Журавского занижает максимальные касательные напряжения почти в два раза.
. Следовательно, формула Журавского занижает максимальные касательные напряжения почти в два раза.
