Многомерные случайные величины
Распределение двумерных случайных величин.
Понятие многомерной случайной величины
Упорядоченный набор  случайных величин называется многомерной (
случайных величин называется многомерной (  мерной) случайной величиной (или системой случайных величин,
мерной) случайной величиной (или системой случайных величин,  мерным вектором).
мерным вектором).
Например погода в данном месте в определённое время суток может быть охарактеризована многомерной случайной величиной  , где
, где  температура,
температура,  влажность,
влажность,  давление,
давление,  скорость ветра и т.п.
скорость ветра и т.п.
Функцией распределения  мерной случайной величины
мерной случайной величины  называется функция
называется функция  , выражающая вероятность совместного выполнения
, выражающая вероятность совместного выполнения  неравенств
неравенств  , т.е
, т.е
 .
.
В дальнейшем ограничимся рассмотрением системы двух случайных величин.
Двумерные случайные величины и их функция распределения
Определение. Законом распределения системы случайных величин называется соотношение, устанавливающее связь между областями возможных значений системы случайных величин и вероятностями появления системы в этих областях.
Определение. Функцией распределения системы двух случайных величин называется функция двух аргументов  , равная вероятности совместного выполнения двух неравенств
, равная вероятности совместного выполнения двух неравенств  :
:
 .
.
Свойства функции распределения системы двух случайных величин.
1) Если один из аргументов стремится к плюс бесконечности, то функция распределения системы стремится к функции распределения одной случайной величины, соответствующей другому аргументу:

 .
.
2) Если оба аргумента стремятся к бесконечности, то функция распределения системы стремится к единице:

2) При стремлении одного или обоих аргументов к минус бесконечности функция распределения стремится к нулю:

4) Функция распределения является неубывающей функцией по каждому аргументу.
5) Вероятность попадания случайной точки 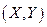 в произвольный прямоугольник со сторонами, параллельными координатным осям, вычисляется по формуле:
в произвольный прямоугольник со сторонами, параллельными координатным осям, вычисляется по формуле:
 .
.
Плотность распределения системы двух случайных величин
Определение.Плотностью совместного распределениявероятностей двумерной случайной величины 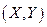 называется вторая смешанная частная производная от функции распределения:
называется вторая смешанная частная производная от функции распределения:
 .
.
Если известна плотность распределения, то функция распределения может быть легко найдена по формуле:
 .
.
Двумерная плотность распределения неотрицательна и двойной интеграл с бесконечными пределами от двумерной плотности равен единице:
 .
.
По известной плотности совместного распределения можно найти плотности распределения каждой из составляющих двумерной случайной величины:

 ;
;  .
.
