Третья задача анализа на чувствительность
Графический анализ допустимого диапазона изменения цен
Изменение цен на продукцию, т.е. изменение коэффициентов ЦФ, представляется на графике вращением целевой прямой вокруг оптимальной точки. Так, при увеличении коэффициента ЦФ 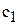 или уменьшении
или уменьшении 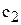 целевая прямая вращается по часовой стрелке. При уменьшении
целевая прямая вращается по часовой стрелке. При уменьшении 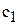 или же увеличении
или же увеличении 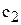 целевая прямая вращается против часовой стрелки (рис.3.4).
целевая прямая вращается против часовой стрелки (рис.3.4).
При таких поворотах точка Е будет оставаться оптимальной до тех пор, пока наклон целевой прямой невыйдет за пределы, определяемые наклонами прямых ограничений (1) и (2). Так, например, если наклон целевой прямой совпадет с наклоном прямой (1), то оптимальным решением будут точки отрезка DE.
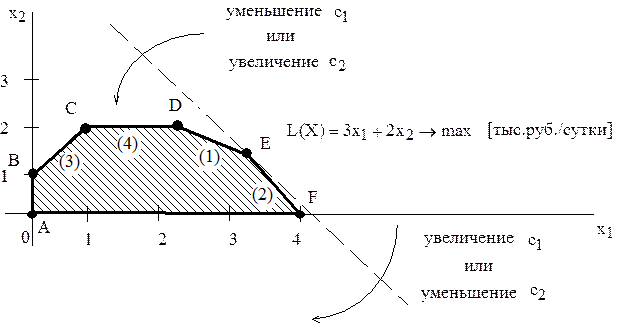
Рис.3.4. Анализ изменения цен
При совпадении c прямой (2) оптимальным решением будут точки отрезка EF. Если целевая прямая выйдет за пределы наклона (1) или (2), то оптимальной точкой станет соответственно D или F.
Допустим, что цена на краску 2-го вида не меняется, т.е. зафиксируем значение целевого коэффициента 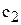 . Проанализируем графически результаты изменения значения целевого коэффициент
. Проанализируем графически результаты изменения значения целевого коэффициент 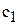 , т.е. цены на краску 1-го вида. Оптимальное решение в точке Е не будет меняться при увеличении
, т.е. цены на краску 1-го вида. Оптимальное решение в точке Е не будет меняться при увеличении 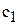 до тех пор, пока целевая прямая не совпадет с прямой (2). Аналогично, оптимальное решение в точке Е не будет меняться при уменьшении
до тех пор, пока целевая прямая не совпадет с прямой (2). Аналогично, оптимальное решение в точке Е не будет меняться при уменьшении 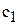 до тех пор, пока целевая прямая не совпадет с прямой (1).
до тех пор, пока целевая прямая не совпадет с прямой (1).
Аналитический поиск допустимого диапазона изменения цен
Совпадение в процессе вращения целевой прямой с прямой ограничения означает, что углы их наклона относительно горизонтальной оси сравнялись, а значит, стали равны тангенсы углов наклона этих прямых.
Правило №3.5
Чтобы определить границы допустимого диапазона изменения коэффициента ЦФ, например 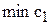 и
и 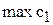 ,
,
необходимо приравнять тангенс угла наклона целевой прямой 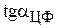 поочередно к тангенсам углов наклона прямых связывающих ограничений, например
поочередно к тангенсам углов наклона прямых связывающих ограничений, например 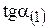 и
и 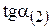 (рис.3.5 и 3.6).
(рис.3.5 и 3.6).
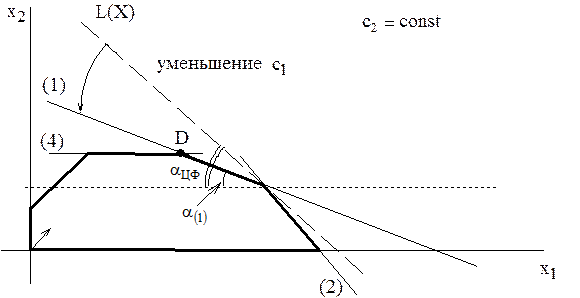
Рис.3.5. Определение 
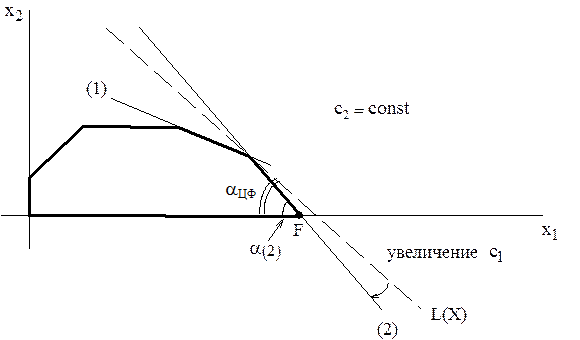
Рис.3.6. Определение 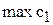
Определим насколько максимально может снизиться цена на краску 1-го вида, не изменяя оптимальную точку Е. Для этого применим правило №3.5 и формулу расчета тангенса угла наклона прямой (рис.3.7).
Рис.3.7. Определение тангенса угла наклона  прямой
прямой 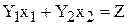
Определим тангенсы углов наклона:
1) целевой прямой 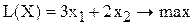 , учитывая, что
, учитывая, что 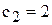 фиксировано
фиксировано
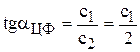 ;
;
2) связывающего ограничения 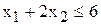 (1)
(1)
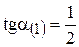 ;
;
3) связывающего ограничения 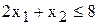 (2)
(2)
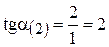 .
.
Для нахождения min 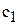 целевая прямая должна совпасть с прямой (1) (см. рис.3.5):
целевая прямая должна совпасть с прямой (1) (см. рис.3.5):
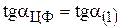 ;
;
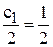 ;
;
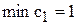 [тыс.руб./т].
[тыс.руб./т].
Для нахождения max 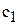 целевая прямая должна совпасть с прямой (2) (см. рис.3.6):
целевая прямая должна совпасть с прямой (2) (см. рис.3.6):
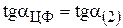 ;
;
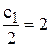 ;
;
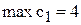 [тыс.руб./т].
[тыс.руб./т].
Таким образом, если цены на краску первого вида будут колебаться в пределах 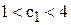 тыс. руб./т, то оптимальное решение задачи не изменится.
тыс. руб./т, то оптимальное решение задачи не изменится.
Из приведенных выше расчетов и графической их иллюстрации следует, что если цена на краску первого вида станет меньше 1 тыс.руб./т ( 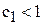 ), то наиболее выгодным будет производство красок в точке D (см. рис.3.5). При этом общее потребление ингредиента В снизится, что приведет к его недефицитности [ресурс (2)], а дефицитными будут ресурсы (1) и (4).
), то наиболее выгодным будет производство красок в точке D (см. рис.3.5). При этом общее потребление ингредиента В снизится, что приведет к его недефицитности [ресурс (2)], а дефицитными будут ресурсы (1) и (4).
Варианты задач для самостоятельного решения
Задача №3.1
Проанализируйте случаи, когда цена на краску первого вида:
1) превысила 4 тыс. руб./т;
2) равна 1 тыс. руб./т;
3) равна 4 тыс. руб./т.
Какая точка станет оптимальной, какими будут объемы производства красок, как изменится дефицитность и объем потребления ресурсов задачи?
Задача №3.2
Определите допустимый диапазон изменения цены на краску 2-го вида при неизменном значении цены на краску первого вида 3 тыс.руб./т в исходной задаче.Проанализируйте влияние изменения цены на краску 2-го вида на объемы производства и дефицитность ресурсов в исходной задаче (аналогично задаче №3.1).
Задача №3.3
Пусть в задаче №1.01 ограничение (1) для ингредиента А изменилось на 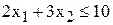 . Определите следующие параметры задачи:
. Определите следующие параметры задачи:
1) новое оптимальное решение 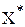 и
и 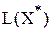 ;
;
2) максимально допустимый прирост объема ингредиента А и соответствующее приращение ЦФ;
3) величины 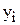 для всех ресурсов задачи.
для всех ресурсов задачи.
Задача №3.4
Пусть в задаче №1.01 ЦФ изменилась на 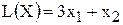 . В этом случае точка F с координатами (4;0) станет оптимальной. Это означает, что краску 2-го вида производить нецелесообразно. Определите, при какой цене или диапазоне цен на краску первого вида станет выгодно производить краску 2-го вида?
. В этом случае точка F с координатами (4;0) станет оптимальной. Это означает, что краску 2-го вида производить нецелесообразно. Определите, при какой цене или диапазоне цен на краску первого вида станет выгодно производить краску 2-го вида?
Задача №3.5
Перечислите виды всех ресурсов и ограничений задачи. Проведите анализ чувствительности оптимального решения для ресурсов (1), (2), (3) и цен 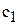 и
и 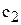 (табл.3.2).
(табл.3.2).
Таблица 3.2
Параметры задачи №3.5
| Модель | Координаты пересечения прямых с осями 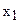 и и 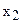 |
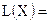 6 6 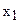 +5 +5 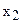  [тыс. руб.] [тыс. руб.] | (2; 2,4) |
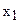 +2 +2 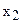 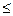 11 [ед. ресурса] (1) 11 [ед. ресурса] (1) | (11; 5,5) |
2 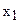 + + 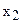 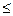 7 [ед. ресурса] (2) 7 [ед. ресурса] (2) | (3,5; 7) |
2 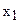 - - 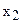 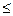 1 [ед. ресурса] (3) 1 [ед. ресурса] (3) | (0,5; -1) |
2 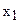 +3 +3 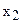 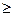 3 [ед. ресурса] (4) 3 [ед. ресурса] (4) | (1,5; 1) |
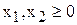 | 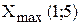 [ед.прод.], [ед.прод.], 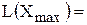 31 [тыс.руб.] 31 [тыс.руб.] |
Задача №3.6*
Используя конкретные примеры моделей задач, сформулируйте задачи, правила, экономическую интерпретацию анализа оптимального решения на чувствительность для следующих случаев:
1) в задаче существуют ограничения со знаком 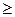 ;
;
2) при поиске допустимого диапазона изменения цены целевая прямая, поворачиваясь вокруг оптимальной точки, проходит через: a) вертикальное положение; b) горизонтальное положение.
Задача №3.7*
Некоторая фирма производит продукцию двух видов с использованием трех видов ресурсов – неравенства (1), (3), (5). Неравенства (2) и (4) ограничивают соответственно минимальный суточный спрос на продукцию первого вида и максимальный суточный спрос на продукцию второго вида. ЦФ представляет собой доход от реализации продукции. Перечислите виды всех ресурсов и ограничений задачи и проведите полный анализ чувствительности оптимального решения (табл.3.3).
Таблица 3.3
Параметры задачи №3.7
| Модель | Координаты пересечения прямых с осями 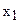 и и 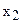 |
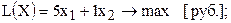 | |
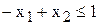 [ед. ресурса] (1) [ед. ресурса] (1) | (-1; 1) |
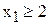 [ед.прод.] (2) [ед.прод.] (2) | (2; –) |
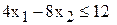 [ед. ресурса] (3) [ед. ресурса] (3) | (3; -1,5) |
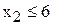 [ед.прод.] (4) [ед.прод.] (4) | (–; 6) |
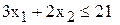 [ед. ресурса] (5) [ед. ресурса] (5) | (7; 10,5) |
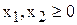 | 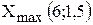 [ед.прод.], [ед.прод.], 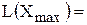 31,5 [руб.] 31,5 [руб.] |
Задача №3.8*
Перечислите виды всех ресурсов и ограничений задачи. Проведите полный анализ чувствительности оптимального решения (табл.3.4).
Таблица 3.4
Параметры задачи №3.8
