Транспортная задача с промежуточными пунктами

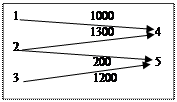
Заводы автомобильной фирмы расположены в Лос-Анжелесе, Детройте, Новом Орлеане. Основные центры оптовой продажи (распределения) продукции сосредоточены в Денвере и Майами. Объемы производства заводов составляют 1000, 1500 и 1200 автомобилей в квартал. Величина квартального спроса в центрах продаж составляет 2300 и 1400 автомобилей. Стоимость перевозок по ж/д одного автомобиля на 1 милю составляет 8 центов. Расстояние между заводами и центрами распределения приведены в таблице

	Денвер (4)	Майами (5)
Лос-Анжелес (1)
Детройт (2)
Новый Орлеан (3)

или если перевести в стоимость перевозки 1 автомобиля

	Денвер (4)	Майами (5)
Лос-Анжелес (1)
Детройт (2)
Новый Орлеан (3)

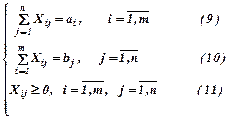
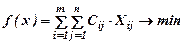
Х14		80	Х15		215
Х24		100	Х25		108
Х34		102	Х35		68

Часто требуется решать транспортную задачу с промежуточными или транзитными пунктами – посредниками.

Допустим возможны перемещения товаров не только от заводов к центрам распределения, но и через склады, принадлежащие 3 заводам. Для осуществления таких транзитных перевозок необходимо предусмотреть емкость складов-буферов в размере 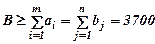. Тогда таблица транспортной задачи и схема перевозок будит иметь вид:

	37000	130	90	100080	215	1000+В=4700
	135	37000	200 101	1300100	109	1500+В=5200
	95	105	35000	102	140065	1200+В=4900
	75	95	110	37000	205	В=3700
	200	107	72	205	37000	В=3700
	В=3700	В=3700	В=3700	2300+В=	1400+В=5100

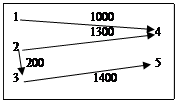
Транспортная сеть

Компания имеет 8 крупных оптовых складов, размещённых в нескольких городах. Отдел сбыта принял решение значительно снизить цену одного дорогостоящего изделия с целью ликвидации образовавшегося запаса этих изделий. Перед началом рекламной компании руководство намерено разместить имеющиеся в наличии запасы на указанных складах в соответствии с прогнозами сбыта в этих районах. Для осуществления этого плана необходимо перераспределить некоторую часть запасов.

Рис. 17. Сеть маршрутов перевозок фирмы.

На рис. 17 показана сеть маршрутов перевозок, причём если из пункта 4 в пункт 5 перевозки осуществляются своим транспортом, а в обратном направлении с помощью наёмного транспорта, то стоимость перевозки единицы груза С₄₅ < С₅₄. В представленной сети имеется один “источник”, из которого существует только исходящий поток грузов, и два “стока”, в которые направлены только входящие потоки грузов. В источнике (пункт 1), а также в пункте 2 имеются избытки запасов, соответственно равные 10 и 2 единицам товара. В стоках (пункты 3 и 8), а также в пункте 6 имеется дефицит товара, соответственно равный 3, 8 и 1 единицам.

В задачах такого типа предложение источника соответствует избытку товара в данном пункте (а₁ = 10), а предложение других пунктов a_k = T_k + S, где T_k – избыток (со знаком +) или спрос (со знаком -) в k-ом пункте, S – суммарное предложение для перемещаемых грузов (S = 10+2=12). Спрос стоков равен потребности в грузах в данных пунктах (b₃ = 3, b₈ = 8), а спрос для других пунктов, равен b_k = S. Решение задачи в виде оптимального плана перевозок при минимуме затрат, представлено на рис. 18.

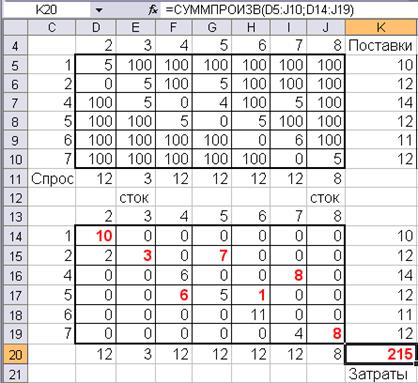
Рис. 18. Исходные данные и оптимальный план перевозок

Задачи с булевыми переменными

Задачи с булевыми переменными (по имени английского математика Джорджа Буля), которые могут принимать значения только δ_i = 0, либо δ_i = 1, - являются частным случаем задач с целочисленными переменными и задач дискретного программирования.

Задачи выбора оптимального варианта или нескольких вариантов из числа заданных решаются с помощью булевых (двоичных) переменных.

Задача. Допустим, рассматриваются четыре проекта, имеющие различные варианта использования ресурсов и различную прибыльность. Имеющиеся в распоряжении фирмы и требуемые для реализации проектов ресурсы (в чел. и ден.ед.), а также ожидаемая прибыль (в ден.ед.) представлены на рис. 19.

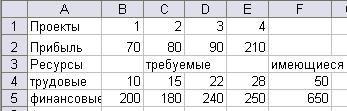
Рис.19. Исходные данные задачи выбора проектов

Математическая модель задачи имеет вид:

,

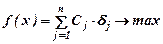
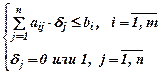где δ_j – булева переменная, C_j – прибыль от реализации j-го проекта, a_ij – ресурсы i-го вида, необходимые для реализации j-го проекта, b_i – имеющийся запас ресурсов i-го вида, m - количество видов ресурсов, n – количество рассматриваемых проектов.

Все цифровые данные необходимо ввести в таблицу Excel, выделить свободные ячейки под искомые значения переменных (В9:Е9) и ввести функцию цели {=СУММПРОИЗВ($B$9:$E$9;B11:E11)} в ячейку F11. В ячейки F13 и F14 ввести выражения для левой части ограничений (рис. 20). В меню Сервис вызвать программу Поиск решения, указать адрес ячейки, содержащей целевую функцию, направление поиска экстремума (max), адреса ячеек, предназначенных для значений искомых переменных. Добавить ограничения по ресурсам и указание на двоичный вид переменных (рис. 21).

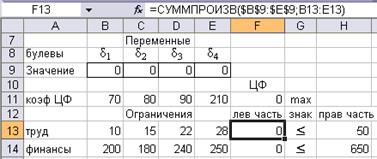
Рис. 20. Формирование математической модели в Excel

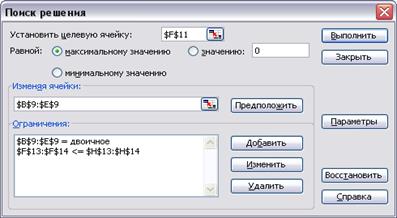
Рис. 21. Ввод условий задачи в программу Поиск решения

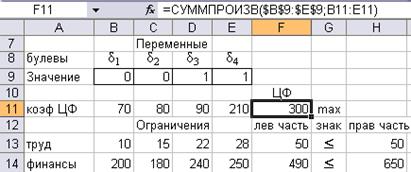
Рис. 22. Результаты решения задачи выбора

Левая часть ограничений является ссылкой на адреса ячеек, содержащих математические выражения, а правая часть ограничений – это ссылка на ячейки, содержащие числовые значения наличного запаса ресурсов. Результаты решения задачи (рис. 22) показывают, что следует выбрать третий и четвёртый проекты, которые принесут максимальную прибыль в количестве 300 ден. ед. Финансовые ресурсы при этом будут использованы не полностью вследствие ограниченного количества трудовых ресурсов, которые будут задействованы полностью.

Использование булевых переменных позволяет вводить в задачу логические условия вида “если…, то…”. Например, если необходимо выбрать из пары вариантов только один (δ_i или δ_j), то логическое условие имеет вид: δ_i + δ_j = 1. Если может быть выбран один вариант и другой, оба вместе или не один из них, то логическое условие имеет вид: δ_i + δ_j ≥ 0. Если при выборе i-го варианта следует принять и j-ый, то логическое условие имеет вид: δ_i = δ_j или δ_i - δ_j = 0. Если при выборе k-го варианта следует принять вариант i, либо j, то логическое условие имеет вид: δ_i + δ_j = δ_k или δ_i + δ_j - δ_k = 0. Если необходимо из четырёх проектов выбрать по крайней мере три, то логическое условие имеет вид: δ₁ + δ₂ + δ₃ + δ₄ ≥ 3.

Использование последнего условия показано на рис. 23.

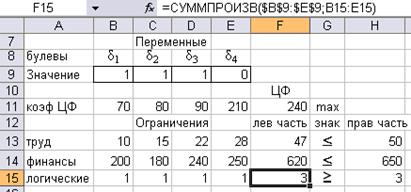
Рис. 23. Результаты решения с логическим ограничением

Результат решения задачи с дополнительным логическим ограничением показывает, что необходимо выбрать первые три проекта, реализация которых принесёт прибыль в размере 240 ден.ед. При этом останутся неизрасходованными трудовые и финансовые ресурсы, но их остатков не хватит для реализации наиболее прибыльного проекта, который требует, впрочем, и наибольших затрат ресурсов.