Раздел 6. Неопределенный интеграл
1. Первообразная. Неопределенный интеграл.
2. Таблица основных интегралов.
3. Основные свойства неопределенного интеграла.
4. Метод замены переменной в неопределенном интеграле.
5. Метод интегрирования по частям.
6. Интегралы от некоторых функций, содержащих квадратный трехчлен.
7. Интегрирование рациональных дробей.
8. Интегрирование иррациональных функций.
9. Интегрирование тригонометрических функций.
10. Вычисление интегралов вида 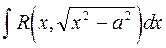 ,
, 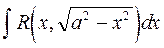 ,
, 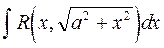 .
.
11. Интегралы, не выражающиеся через элементарные функции.
Раздел 7. Определенный интеграл
1. Задачи геометрического, физического и экономического содержания, приводящие к понятию определенного интеграла.
2. Определение определенного интеграла. Основные свойства.
3. Теорема об интеграле с переменным верхним пределом.
4. Формула Ньютона - Лейбница.
5. Замена переменной в определенном интеграле.
6. Интегрирование по частям при вычислении определенного интеграла.
7. Вычисление площадей плоских фигур в прямоугольных координатах.
8. Вычисление площадей плоских фигур в полярных координатах.
9. Вычисление длины дуги плоской кривой.
10. Вычисление объема тела по площадям параллельных сечений.
11. Объем тела вращения.
12 Применения определенного интеграла в экономике.
13. Интегралы с бесконечными пределами интегрирования.
14. Интегралы от неограниченных функций.
15. Признаки сходимости несобственных интегралов.
Раздел 8. Дифференциальные уравнения
1. Обыкновенные дифференциальные уравнения (основные понятия).
2. Дифференциальные уравнения первого порядка. Задача Коши. Теорема существования и единственности решения задачи Коши (формулировка).
3. Дифференциальные уравнения с разделяющимися переменными.
4. Дифференциальные уравнения с однородными функциями.
5. Линейные дифференциальные уравнения первого порядка и уравнения Бернулли.
6. Дифференциальные уравнения высших порядков, допускающие понижение порядка.
7. Линейные однородные уравнения n-го порядка; свойства их решений.
8. Теорема о структуре общего решения линейного однородного дифференциального уравнения.
9. Теорема о структуре общего решения линейного неоднородного дифференциального уравнения.
10. Линейные однородные дифференциальные уравнения с постоянными коэффициентами.
11. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами и правой частью специального вида.
Раздел 9. Ряды
1. Числовой ряд. Сумма и остаток ряда.
2. Необходимый признак сходимости ряда.
3. Сравнение рядов с положительными членами.
4. Достаточные признаки сходимости Даламбера и Коши.
5. Интегральный признак Коши.
6. Знакочередующиеся ряды. Признак Лейбница.
7. Знакопеременные ряды. Абсолютная и условная сходимость.
8. Степенные ряды. Теорема Абеля. Интервал и радиус сходимости.
9. Свойства степенных рядов.
10. Ряды Тейлора и Маклорена.
11.Разложение функций sin x, cos x, ex, ln(1±x), (1+x)mв ряды Маклорена.
12. Применение степенных рядов в приближенных вычислениях.
