Синтез управления системы с неопределенными нелинейностями и внешними неопределенными ограниченными возмущениями

Задача синтеза управления в виде обратной связи по состоянию 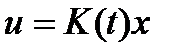, стабилизирующего замкнутую систему и подавляющего начальные отклонения и воздействие внешних возмущений в смысле минимальности ограничивающего эллипсоида для выхода z сводится к оптимизации критерия при ограничениях в виде дифференциальных линейных матричных неравенств. В качестве критерия берется след матрицы, определяющей размер инвариантного или ограничивающего выход эллипсоида.

Теорема 3.3. Решение задачи

при ограничениях

, (12)

, (13)

где минимизация проводится по матричным переменным , скалярной переменной β>0 и скалярному параметру , определяет при каждом матрицу ограничивающего эллипсоида для вектора состояния x(t), матрицу ограничивающего эллипсоида для вектора выхода z(t) системы (3.1) и зависимую от времени матрицу коэффициентов соответствующего регулятора по состоянию . Если, кроме того, матрица удовлетворяет дополнительно ограничениям и для всех , где R и S(t) – заданные положительно определенные симметрические матрицы, то искомый регулятор обеспечивает ограниченность замкнутой системы относительно множеств [E(R), E_w(I), E(S(t))] при всех нелинейностях из (3.2).

В случае неполного измерения вектора состояния для реализации закона управления в виде обратной связи по состоянию могут быть использованы наблюдатели состояния, рассмотренные в п.2.1 и 2.2.

Рассмотрим снова пример из п.3.1, в котором вместо конкретной нелинейности присутствует неопределенная нелинейность , удовлетворяющая неравенству (3.2) с параметрами и и .

Ниже представлен текст программы на входном языке пакета MatLab для синтеза регулятора по состоянию на основе решения задачи оптимизации с линейными матричными неравенствами

% Пример синтеза, оценивания состояния и моделирования

%--Исходные данные -- модель с неопределенными нелинейностями и возмущениями

% Параметры регулятора u=k1x2+k2x4

% вектор состояния x=(x1,x2)T

n=2;

n1=n;

%параметры

w=0.5;

mu1=1;

%--матрицы системы---

A = [0 1; 0 0];

B1 = [0; 1];

D=[0; 1];

C=[1 0;0 1;0 0];

B2=[0; 0;1];

F=[0; -w*w];

CF=[1; 0];

eig(A)

% Синтез регулятора по состоянию на основе решение линейных матричных

% неравенств

step = 0.1;

begin_val = 0.4;%0.1;%

end_val = 2.0;%0.2;%-min(eig(A-B*K));

min_tr_Q = 1000000;

figure (1)

% Оптимизация по параметру q путем перебора с уменьшающимся шагом

while step>0.001

for q = begin_val:step:end_val

cvx_begin sdp

variable Qs(n1, n1) symmetric;

variable Zs(1,1) symmetric;

variable Ys(1, n1) ;

variable bet ;

minimize( trace(C*Qs*C'+C*Ys'*B2'+B2*Ys*C'+B2*Zs*B2'))

%minimize( trace(Qs))

subject to

Qs >= eye(2)*10e-3;

[A*Qs + Qs*A'+B1*Ys+Ys'*B1'+q*Qs+bet*(F*F') D Qs*CF;

D' -q 0;

CF’*Qs 0 -(bet/mu1)]< 0; %условие асимптотической устойчивости

[Zs Ys;

Ys' Qs]>=0;

% [Qs eye(4); eye(4) 1500*eye(4)]>0;

%norm(Ys, 'fro')<=1000;

cvx_end

Qsf = double(Qs)

Y=double(Ys)

K=Y/Qsf

Z=double(Zs);

ABK=A+B1*K

eig(ABK)

%trZ=trace(Qsf);

trZ=trace(C*Qsf*C'+C*Y'*B2'+B2*Y*C'+B2*Z*B2');

if min_tr_Q > trZ

min_tr_Q = trZ

Q_min = Qsf;

K_min=K;

q_min = q

bet_min=bet;

end;

end;

step = step*0.5;

begin_val = q_min-2*step;

end_val = q_min+2*step;

end;

Qsf=Q_min

K=K_min

q=q_min

bet=bet_min;

ABK=A+B1*K;

bet1=bet;

ABKI=ABK;

beti=bet;

С помощью данной программы при q=2.697, β=0.1352 была найдена матрица K=[–9.1806 –5.8861] -коэффициентов регулятора по состоянию. При этом матрица замкнутой системы имеет собственные значения –2.9431±0.7204i -и является гурвицевой. Получена следующая матрица минимального предельного инвариантного эллипсоида:

.

Также с помощью решения задачи оптимизации с ЛМН была получена матрица максимального инвариантного эллипсоида, лежащего в области притяжения исходной нелинейной системы. Для этого использовался следующий фрагмент программы

% Решение линейных матричных неравенств инвариантный эллипсоид из области

% притяжения матричной СС (с Регулятором по состоянию)

cvx_begin sdp

variable Qs(n1, n1) symmetric;

minimize(trace(-Qs))

subject to

Qs >= eye(2)*10e-2;

[ABK*Qs + Qs*ABK'+q*Qs+bet1*(F*F') D Qs*CF;

D' -q 0;

CF’*Qs 0 -(bet/mu1)]< 0; %условие асимптотич устойчивости

cvx_end

Qsf1 = double(Qs)

E = ellipsoid(Qsf);

%pEs = projection(E, BB);

plot(E,'b'); hold on;grid on;

E = ellipsoid(Qsf1);

%pEs = projection(E, BB);

plot(E,'r'); hold on;grid on;

На рисунке 3.1 показаны минимальный предельный инвариантный эллипс и максимальный инвариантный эллипс из области притяжения исходной системы.

Рисунок 3.1. Минимальный предельный инвариантный эллипс (синяя сплошная линия) и инвариантный эллипс из области притяжения (красная сплошная линия)

Рисунок 3.2. Сечения эволюционирующего инвариантного эллипса

На рисунке 3.2 показаны сечения эволюционирующего инвариантного эллипса, полученные на основе численного интегрирования МСС с начальной матрицей

.

Частное решение МСС сошлось за T<10c к минимальному инвариантному эллипсу с матрицей . Программа для построения эллипсоидальных оценок с помощью МСС представлена ниже.

Q=(Qsf01+Qsf1)/2;

vec_Q = [Q(:,1); Q(:,2)];

[t,H] = ode15s(@PravSyntLMI25102014,[0 10],vec_Q);

hs = size(H);

MQ1 = [];

nh=length(H(:,1))

t(nh)

nn=1

figure (11)

for i = 1:nn:nh

MQ1 = [H(i,1) H(i,2); H(i,3) H(i,4)];

MQ1=(MQ1+MQ1')/2;

E = ellipsoid(MQ1);

%pEs = projection(E, BB);

plot(E, 'b');grid on;hold on;

end;

plot(E, 'r');grid on;hold on;

Для вычисления правой части матричной системы сравнения используется следующая функция.

function dQ=PravSyntLMI25102014(t,vec_Q)

% Вычисление правой части матричной системы сравнения и определение матрицы

% коэффициентов усиления регулятора в текущий момент времени

global ABK D q bet mu1 F CF

Q = [ vec_Q(1) vec_Q(2); vec_Q(3) vec_Q(4)];

dQQ= ABK*Q + Q*ABK' +q*Q+(D*D')/q+bet*(F*F')+mu1*Q*(CF*CF')*Q/bet;

dQQ=(dQQ+dQQ')/2;

dQ = reshape(dQQ,4,1);

На основе теоремы 3.3 был получен регулятор в виде обратной связи по состоянию с зависимыми от времени коэффициентами усиления. Для этого были решены на интервале [0,10c] ДЛМН (12) с начальной матрицей

и с оптимизацией на каждом шаге ограничивающего эллипсоида для выхода при ограничениях ЛМН (13). Текст программы для численного решения ДЛМН (12) с ЛМН (13) с оптимизацией на каждом шаге дискретизации представлена ниже.

k=1;

kend=200;

e=0.1;

t(k)=0;

figure (2)

Q0=Qsf1+[0.5 0;0 2];

KK=[];

while k<kend

E = ellipsoid(Q0);

% pEs = projection(E, BB);

plot(E, 'b');grid on;hold on;

t(k)=(k-1)*e;

cvx_begin sdp

variable Qs(n1, n1) symmetric;

variable Zs(1,1) symmetric;

variable Ys5(1, n1) ;

variable bet5 ;

minimize( trace(C*(Q0-Qs*e)*C'+C*Ys5'*B2'+B2*Ys5*C'+B2*Zs*B2'))

%minimize( trace(Q0-Qs*e))

subject to

Qs >= Q0/4;

%(Q0-Qs*e)>=0;

[Qs+(A*(Q0-Qs*e)+(Q0-Qs*e)*A'+B1*Ys5+Ys5'*B1'+q*(Q0-Qs*e)+bet5*(F*F')) D (Q0-Qs*e)*CF;

D' -q 0;

CF'*(Q0-Qs*e) 0 -(bet5/mu1)]< 0; %условие асимптотич устойчивости

[Zs Ys5;

Ys5' Q0-Qs*e]>=eye(3)*10e-5;

cvx_end

Qsf5 = double(Qs);

Y5=double(Ys5);

bet05=double(bet5);

betk(k)=bet05;

Q0=Q0-Qsf5*e

E = ellipsoid(Q0);

plot(E, 'b');grid on;hold on;

K5=Y5/Q0;

KK1(k)=K5(1);

KK2(k)=K5(2);

ABK5=A+B1*K5;

%eig(ABK5);

k=k+1;

tk=k*e

end;

E = ellipsoid(Q0);

plot(E, 'r');grid on;hold on;

figure (7)

plot(t,betk,'r');grid on;hold on;

plot(t,KK1,'b');grid on;hold on;

plot(t,KK2,'g');grid on;hold on;

На рисунке 3.3 показаны эллипсы, являющиеся сечениями в моменты времени t_k, k=1,…,200, t₁=0, t_k+1=t_k+0.1 эволюционирующего инвариантного эллипса. Начальный эллипс (k=1) обозначен штрих пунктирной линией, а конечный эллипс (k=200) обозначен сплошной линией. Ему соответствует матрица

.

Рисунок 3.3. Сечения эволюционирующего инвариантного эллипса для рассматриваемой системы с регулятором, коэффициенты усиления которого зависят от времени.

На рисунке 3.4 показаны графики изменения параметра β(t) (сплошной линией), значения которого сначала возрастают, а затем монотонно убывают, и коэффициентов усиления K₁(t) и K₂(t) регулятора (показаны штриховой и штрих пунктирной линией соответственно). Если после 10с оставить регулятор с постоянными коэффициентами усиления K2=[–17.9843 –6.9976], полученными на последнем шаге, то для рассматриваемой нелинейной системы с таким регулятором, матрица минимального инвариантного эллипса определится

.

Получена также матрица инвариантного эллипса из области притяжения

Рисунок 3.4. Изменение параметра β и коэффициентов усиления регулятора во времени

Для реализации закона управления в виде обратной связи по состоянию при неполной информации о векторе состояния следует использовать наблюдатели для получения оценок полного вектора состояний по результатам измерения вектора выхода. Способы построения наблюдателей состояния для систем с неопределенными возмущениями и примеры их использования для реализации законов управления по состоянию представлены в разделе 2.

4. Пример решения задач ограниченности относительно заданных множеств, качества по H_¥ критерию и синтеза управления в виде обратной связи по состоянию для простейшей системы с неопределенными нелинейностями и возмущениями

Постановка задачи

Рассматривается динамическая система, представленная следующей моделью в пространстве состояний в непрерывном случае

(4.1)

где 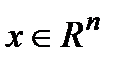- вектор состояния, 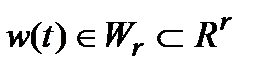- входное возмущение, - вектор управляемого выхода, - известные матрицы с непрерывными и ограниченными элементами при всех , T>0 заданная константа (при рассмотрении на конечном интервале) или T=¥ (при рассмотрении на бесконечном интервале).

Нелинейная векторная функция удовлетворяет условию, заданному в виде:

(4.2)

где - известная матрица с непрерывными и ограниченными элементами при всех . Здесь и далее означает евклидову норму вектора, - заданный параметр.

Предположим, что неопределенные возмущения являются непрерывными ограниченными по L₂ норме функциями времени:

, (4.3)

где и - известные константа и функция времени соответственно.

Множество таких функций w обозначим W.

Важное отличие от рассмотренного в предыдущих разделах случае является то, что здесь рассматривается другой класс возмущений, т.е. возмущения с конечной энергией (удовлетворяющие интегральному ограничению (4)).

Для рассматриваемой системы ставятся задача анализа ограниченности на конечном интервале относительно заданных множеств начальных отклонений и допустимых текущих состояний.