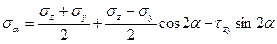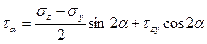Рациональные формы поперечных сечений упругих балок (прямых брусьев) при прямом чистом изгибе. Привести примеры
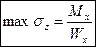
Для прямоугольного сечения: 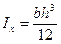 ,
, 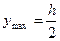 ,
, 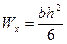 .
.
Для круглого сечения: 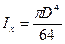 ,
, 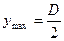 ,
, 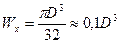 .
.
Таким образом, напряжения при изгибе обратно пропорциональны третьей степени линейных размеров сечения.
Прямой поперечный изгиб балки (прямого бруса). Вывод формулы Д.И.Журавского для определения касательных напряжений, возникающих в симметричных поперечных сечениях балки при условии, что силовая линия совпадает с осью симметрии поперечного сечения балки. Вывод формулы для определения касательных напряжений в прямоугольном поперечном сечении балки с использованием формулы Д.И.Журавского.
Поперечный изгиб балки – такой изгиб балки, при котором в сечениях помимо изгибающего момента возникает поперечные силы.
Если силовая линия совпадает с одной из главных центральных осей инерции поперечного сечения балки, изгиб называется прямым.
Прямой поперечный изгиб реализуется тогда, когда силовая линия совпадает с главной центральной осью инерции (осью у) и в поперечном сечении возникают поперечные силы, а у≠0 и изгибающий момент Мх≠0.
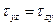
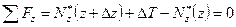
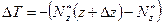
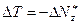 (1)
(1)
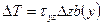 (2)
(2)
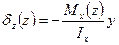 ,
, 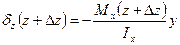
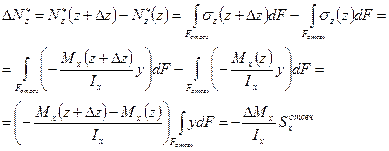 (3) – статический момент отсечённой части площади поперечного сечения относительно оси х (нейтральной линии).
(3) – статический момент отсечённой части площади поперечного сечения относительно оси х (нейтральной линии).
Подставим в (1), (2), (3):
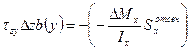 ,
, 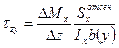
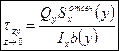 - формула Журавского для вычисления касательных напряжений в поперечном сечении балки при прямом поперечном изгибе.
- формула Журавского для вычисления касательных напряжений в поперечном сечении балки при прямом поперечном изгибе.
Расчёт касательных напряжений в прямоугольном поперечном сечении балки с использованием формулы Д.И.Журавского:
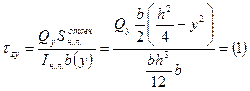
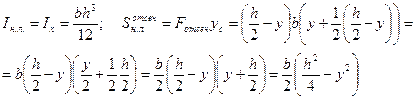
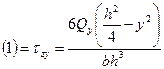 ,
, 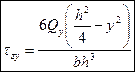 .
.
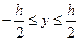 при у=0
при у=0 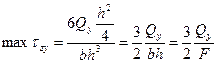
при 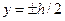
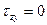 .
.
Прямой поперечный изгиб балки (прямого бруса). Вывод формулы для определения касательных напряжений, возникающих в поперечных сечениях двутавровой балки с использованием формулы Д.И.Журавского.
Прямой поперечный изгиб балки (прямого бруса) см. в вопросе 31.
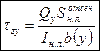
Iн.л.=Ix – находится по таблице.
b(y)=d – находится по таблице.
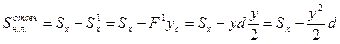
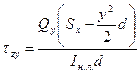
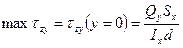 ,
, 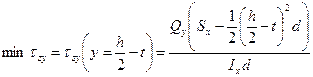
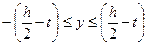 .
.
Условие прочности при прямом поперечном изгибе балки.
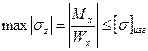 ,
,
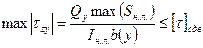 .
.
Сравнительная оценка величин максимальных по модулю нормальных и касательных напряжений, возникающих в поперечных сечениях балки при прямом поперечном изгибе.
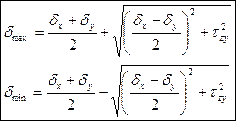 ,
,
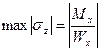 ,
,
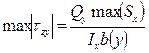 .
.
Работа внешнего изгибающего момента при прямом чистом изгибе линейно-упругого бруса.
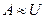
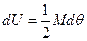 , но
, но 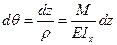 , отсюда:
, отсюда: 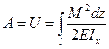 .
.
Вывод формулы потенциальной энергии упругой деформации прямого бруса при чистом прямом изгибе. Выражение работы внешнего изгибающего момента через потенциальную энергию упругой деформации бруса.
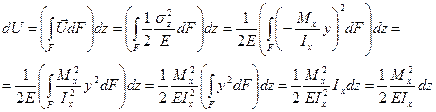
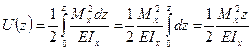
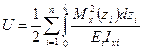 ,
, 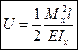 ,
, 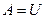 .
. 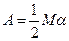 ,
,
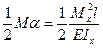 ,
, 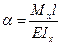 .
.
Потенциальная энергия прямого бруса при прямом поперечном изгибе.
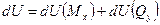
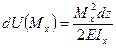 ,
, 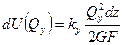 ,
, 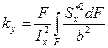 ,
, 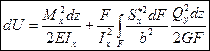 .
.
Плоское напряжённое состояние в точке. Аналитическое исследование нормальных и касательных напряжений, возникающих в произвольно задаваемых площадках, перпендикулярных плоскости действия заданных напряжений.
Выделяем из сплошной линейно-упругой среды бесконечно малый объём тремя парами ортогональных площадок (в частности - взаимно перпендикулярных плоскостейыделяем из сплошной линейно-упругой среды бесконечно малый объём тремя парами ортогональных площадок ()Д.И.()вается прямым.
).