Interpol_Lagrang(n, x, y, q);

6. вывести на экран терминала (в текстовый файл) вектор коэффициентов.

Пример: определить коэффициенты интерполяционного полинома Лагранжа для функции, заданной в четырех точках:

x	23,3	24,25	25,25	26,1
y

Головная программа:

#include <stdio.h>

#include <math.h>

#include <conio.h>

void interpol_Lagrang(int n, float x[n], float y[n], float q[n]);

int main(int argc, char **argv)

{

int n;// количество узлов интерполяции

int i;// рабочая переменная

printf("\n uzlov interpoljacii n= ");

scanf("%d", &n);

float x[n], y[n];// исходные узлы интерполяции

float q[n];// массив коэффициентов

//интерполяционного полинома Лагранжа

// по возрастанию степеней

printf("\nVvedite vector argumenta (%d znacheniy):\n", n);

for (i=0; i<n; i++)

scanf("%f", &x[i]);

printf("\n");

printf("\nVvedite vector funkcii (%d znacheniy):\n", n);

for (i=0; i<n; i++)

scanf("%f", &y[i]);

printf("\n");

Interpol_Lagrang(n, x, y, q);

printf("\nKoefficienty interpol. polinoma Lagranga po vozrast. stepeney:\n");

for (i=0; i<n; i++)

printf("%10.3f", q[i]);

printf("\n");

Return 0;

}

Результат работы программы:

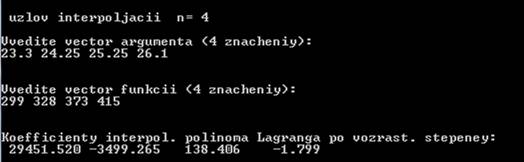
Таким образом, интерполяционный полином Лагранжа имеет вид:

29451,52 – 3499,265x + 138,406x² – 1,799x³

Интерполяция функций, заданных аналитически,
рядом Фурье

В головной программе необходимо:

1. описать прототип интерполирующей функции:

int Furie_interpol_analit(int n, float a[], float b[]);

1. ввести значение переменной n – количество слагаемых ряда Фурье,
2. описать выходные массивы:

float a[n];// коэффициенты ряда Фурье при cos(), начиная с // нулевого (n+1 коэффициент)

float b[n];// коэффициенты ряда Фурье при sin(), начиная с // нулевого (n+1 коэффициент)

1. обратиться к программе расчета коэффициентов:

Furie_interpol_analit(n, a, b);

1. вывести на экран терминала (в текстовый файл) массивы коэффициентов ряда Фурье.

В функции float function(float x) описать исходную функцию в виде f=f(x), например:

Float function(float x)

{

Float f;

f=x*x;

if(x>M_PI)

f=(2.0*M_PI-x)*(2.0*M_PI-x);

Return f;

}

Пример: найти коэффициенты ряда Фурье для функции

x² , если x≤π,

f(x)=

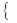
(2π – x), если x>π.

Ряд Фурье для этой функции имеет вид:

f(x) = 3,289868 – 4/1! cos(x) + 4/2! cos(2x) – 4/3! cos(3x) + 4/4! cos(4x) - …

Головная программа:

#include <stdio.h>

#include <math.h>

#include <conio.h>

int Furie_interpol_analit(int n, float a[], float b[]);

int main(int argc, char **argv)

{

int n;// количество слагаемых ряда Фурье

int i;// рабочая переменная

printf("\n Kol-vo slagaem. n=");

scanf("%d", &n);

float a[n];//коэффициенты ряда Фурье при cos(),

//начиная с нулевого (n+1 коэффициент)

float b[n];//коэффициенты ряда Фурье при sin(),

//начиная с нулевого (n+1 коэффициент)