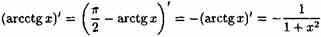Производные основных элементарных функций
1)Степенная функция у=x^n, n є N
Дадим аргументу х приращение ∆х. Функция у=х^n получит приращение ∆у=(х+∆х)^n-x^n. По формуле бинома Ньютона имеем
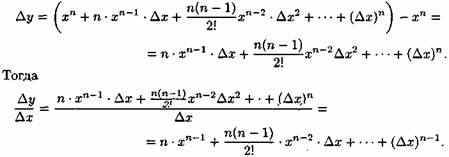
Находим предел составленного отношения при ∆х→0:
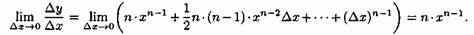
Таким образом,(х^n)=n•х^(n-1)
Ниже будет показано, что формула производной степенной функции справедлива при любом n є R (а не только натуральном).
2)Показательная функция у=а^х, а>0, а≠1
Найдем сначала производную функции у=ех. Придав аргументу х приращение ∆х, находим приращение функции ∆у: ∆у=е^(х+∆х)-е^х =е^х(е^(∆х-1)). Стало быть,
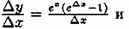
При вычислении предела воспользовались эквивалентностью е^х-l~x при х→0.
Итак, у'=е^х, т.е.
(e^x)'=e^x
Теперь рассмотрим функцию у=а^х, х є R. Так как а^х=e^(xlna), то по формуле производной сложной функции находим:
(а^x)'=(е^(хlnа))'=e^(xlna)•(х•lna)'=е^(хlnа)•lna=a^x•lnа.
Таким образом, (a^х)'=a^х Inа.
Производная сложной и обратной функций
Пусть у=ƒ(u) и u=φ(х), тогда у=ƒ(φ(х)) — сложная функция с промежуточным аргументом u и независимым аргументом х.
Теорема 20.5 . Если функция u=φ(х) имеет производную u'х в точке х, а функция у=ƒ(u) имеет производную у'u в соответствующей точке u=φ(х), то сложная функция у=ƒ(φ(х)) имеет производную у'х в точке х, которая находится по формуле у'х=у'u-u'х.
По условию
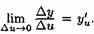
Отсюда, по теореме о связи функции, ее предела и бесконечно малой функции, имеем
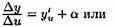∆у=у'u•∆u+α*∆u, (20.6)
где α→0 при ∆u→0.
Функция u=φ(х) имеет производную в точке х:
поэтому
∆u=u¢ х •∆х+ß•∆х, где ß→0 при ∆х→0.
Подставив значение ∆u в равенство (20.6), получим
Δy=y¢ u(u'х•∆х+ß*∆х)+а(u'х•∆х+ß•∆х),
т.е.
∆у=у'u•u'х•∆х+у'u•ß•∆х+u'х•а•∆х+α•ß•∆х.
Разделив полученное равенство на ∆х и перейдя к пределу при ∆х→О, получим у'х=у'u*u'х.
Итак, для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножыть на производную промежуточного аргумента по независимому аргументу.
Это правило остается в силе, если промежуточных аргументов несколько. Так, если у=ƒ(u), u=φ(ν), ν=g(х), то у'х=у'u•u'ν•ν'х. Пусть у=ƒ(х) и х=φ(у) — взаимно обратные функции.
Теорема 20.6 . Если функция у=ƒ(х) строго монотонна на интервале (a;b) и имеет неравную нулю производную ƒ'(х) в произвольной точке этого интервала, то обратная ей функция х=φ(у) также имеет производную φ'(у) в соответствующей точке, определяемую равенством
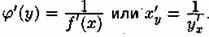
Рассмотрим обратную функцию х=φ(у). Дадим аргументу у приращение ∆у¹ 0. Ему соответствует приращение ∆х обратной функции, причем ∆х¹ 0 в силу строгой монотонности функции у=ƒ(х). Поэтому можно записать
Если ∆у→0, то в силу непрерывности обратной функции приращение ∆х→0. И так как
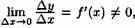
то из (20.7) следуют равенства
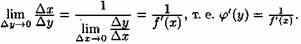
Таким образом, производная обратной функции равна обратной величине производной данной функции.
Правило дифференцирования обратной функции записывают так:
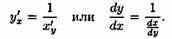
Обратные тригонометрические функции у=arcsinx, у=arccosx, y=arctgх, у=arcctgx
Пусть у=arcsinx. Обратная ей функция имеет вид x=siny, ує[-p/2; p /2]. На интервале (-p /2;p/2) верно равенство x'=cosy≠0.
По правилу дифференцирования обратных функций
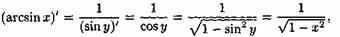
где перед корнем взят знак плюс, так как cosy>0 при у є(-p /2;p/2).
Итак,
Аналогично получаем, что
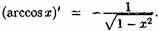
Эту формулу можно получить проще: так как arccosх+arcsinх=p/2, т.е. arccosx=p/2-arcsinх, то (arccosx)'=(p /2-arcsinх)=-1/Ö (1-х2)
Найдем производную функции у=arctgx.
Она является обратной к функции х=tgy, где ує(-p/2;p /2).
Поэтому, по правилу дифференцирования обратных функций, получаем, что
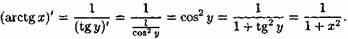
Итак,
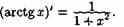
Функции arctgх и arcctgх связаны отношением
arctgx+arcctgх=p /2, т. е. arcctgх=p /2-arctgx.
Дифференцируя это равенство, находим
