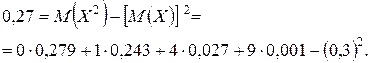Дискретных случайных величин

[1], Гл. VI

Случайной называют величину, которая в результате опыта принимает одно из возможных значений, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.

Различают два вида случайных величин: дискретные и непрерывные.

Дискретной называется такая случайная величина, которая в результате опыта может принимать отдельные числовые значения, которые можно перенумеровать.

Непрерывная случайная величина принимает значения, которые сплошь заполняют некоторый промежуток.

Промежуток может вырождаться в точку или совпадать со всей числовой осью.

Законом распределения дискретной случайной величины называют перечень всех значений с их вероятностями. Последние могут быть найдены по формуле Пуассона, по формуле Бернулли, непосредственным подсчетом вероятностей и т.д. Сумма вероятностей всех возможных значений дискретной случайной величины равна единице.

Закон распределения можно изобразить таблично:

X	x1	x2	x3	…	xn
P	p1	p2	p3	…	pn

где .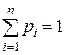

Закон распределения можно изобразить графически. С этой целью в системе координат по оси Ox откладывают значения дискретной случайной величины, а по оси Oy – соответствующие вероятности. Полученные точки 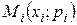соединяют отрезками прямых. Полученную фигуру называют многоугольником распределения.

Числовые характеристики дискретных

Случайных величин

[1], Гл. VII, VIII

Часто закон распределения случайной величины неизвестен и приходится ограничиваться меньшими сведениями.

Пользуются числовыми характеристиками положения случайной величины, к числу которых относятся, прежде всего, математическое ожидание и дисперсия.

Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее значений на их вероятности. Обозначают: .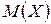

.

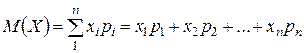Математическое ожидание – это среднее ожидаемое значение случайной величины. Его размерность совпадает с размерностью случайной величины. Математическое ожидание случайной величины есть неслучайная (постоянная величина), которая может принимать любые числовые значения для любых случайных величин.

Дисперсией случайной величины называют математическое ожидание квадратов отклонений случайной величины от ее математического ожидания. Обозначают: .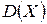

.

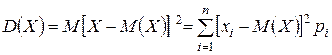Иногда бывает проще применить формулу

.

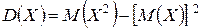Дисперсия может принимать только неотрицательные числовые значения. Если 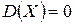, то величина 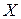- постоянна. Размерность дисперсии совпадает с квадратом размерности случайной величины 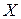. Для получения характеристики разброса случайной величины вокруг ее среднего значения используют также среднее квадратическое отклонение

.

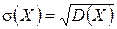Его размерность уже совпадает с размерностью изучаемой случайной величины. Если проведено n независимых испытаний и вероятность появления события в каждом испытании постоянна и равна p, то

,

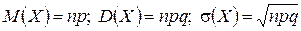где 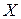- число появлений события А при n испытаниях.

Задача 1

Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте. Найти числовые характеристики и построить многоугольник распределения.

Р е ш е н и е

Число отказавших элементов в одном опыте – дискретная случайная величина X, которая принимает следующие значения: 0,1,2,3.

Отказы независимы между собой, вероятности отказа каждого элемента равны между собой, тогда вероятности отдельных значений можно найти по формуле Бернулли:

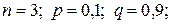
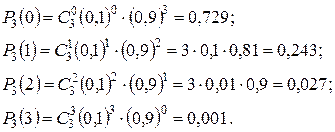
Контроль: .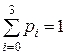

Напишем искомый биномиальный закон распределения :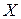

X
P	0,729	0,243	0,027	0,001

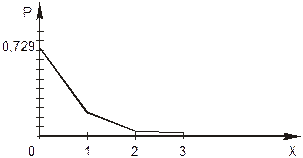Построим многоугольник распределения:

Для нахождения числовых характеристик воспользуемся формулами, имеющими место для биномиального распределения:

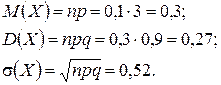
Полезно убедиться, что эти же значения получаем по определению 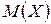и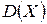

;
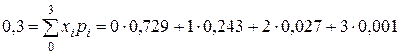