Алгоритм симплексного метода
Включает следующие шаги:
1 шаг. Составление первого опорного плана.
Система ограничений задачи задана в виде системы неравенств. Перейдём от системы неравенств к системе уравнений путём введения неотрицательных дополнительных переменных, т.е. приведём математическую модель задачи к каноническому виду. Вектор-столбцы при этих переменных представляют собой единичные векторы и образуют базис, а соответствующие им переменные называются базисными:
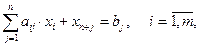 где xj – свободные переменные, xh+i - базисные переменные.
где xj – свободные переменные, xh+i - базисные переменные.
Решаем эту систему относительно базисных переменных:
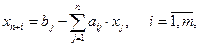
а функцию цели перепишем в виде:
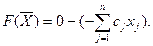
Полагая, что основные переменные x1= x2= x3=…= xn=0, получим первый опорный план
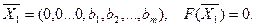
Заполняем первую симплексную таблицу, которая состоит из коэффициентов системы ограничений и свободных членов. Последнюю индексную строку заполняем коэффициентами целевой функции, взятыми с противоположными знаками.
2 шаг. Проверка плана на оптимальность.
Если все коэффициенты индексной строки симплексной таблицы первого плана 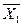 при решении задачи на максимум неотрицательны, то план
при решении задачи на максимум неотрицательны, то план 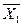 , является оптимальным и задача решена. Если найдётся хотя бы один отрицательный коэффициент в индексной строке, то план
, является оптимальным и задача решена. Если найдётся хотя бы один отрицательный коэффициент в индексной строке, то план 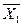 - не оптимальный и его можно улучшить.
- не оптимальный и его можно улучшить.
3 шаг. Определение ведущего столбца, ведущей строки, разрешающего элемента.
Из отрицательных элементов индексной строки выбираем «наихудший» (наибольший по абсолютной величине), он определяет ведущий столбец (заштриховать), который показывает, какая переменная на следующей итерации перейдёт из свободных в базисные.
Затем элементы столбца свободных членов 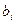 симплексной таблицы делим на соответствующие положительные элементы ведущего столбца.
симплексной таблицы делим на соответствующие положительные элементы ведущего столбца.
Введём дополнительный столбец 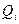 , в который запишем результаты данного деления. Минимальное значение столбца
, в который запишем результаты данного деления. Минимальное значение столбца 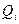 определяет переменную
определяет переменную 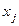 , которая на следующей итерации выйдет из базиса и станет свободной.
, которая на следующей итерации выйдет из базиса и станет свободной.
На пересечении ведущего столбца и ведущей строки находится разрешающий элемент (выделяем кружком).
4 шаг. Построение нового опорного плана.
Строим новую таблицу плана 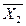 . Для этого все элементы ведущей строки делим на разрешающий элемент, результаты заносим в новую таблицу. Заполняем базисные столбцы. Остальные элементы нового плана находим по правилу «прямоугольника»:
. Для этого все элементы ведущей строки делим на разрешающий элемент, результаты заносим в новую таблицу. Заполняем базисные столбцы. Остальные элементы нового плана находим по правилу «прямоугольника»:






 А РЭ
А РЭ 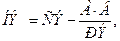
 |  | ||
 НЭ(СЭ) В
НЭ(СЭ) В
где НЭ – новый элемент, СЭ – старый элемент, РЭ – разрешающий элемент, А и В – элементы старого плана, составляющие диагональ, противоположную диагонали СЭ-РЭ.
5 шаг. Проверка на оптимальность нового плана.
План 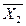 проверяется на оптимальность в соответствии с шагом 2, делается вывод об оптимальности второго плана
проверяется на оптимальность в соответствии с шагом 2, делается вывод об оптимальности второго плана 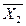 или, в противном случае, улучшение плана
или, в противном случае, улучшение плана 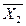 продолжается аналогично до тех пор, пока в индексной строке не останется отрицательных коэффициентов.
продолжается аналогично до тех пор, пока в индексной строке не останется отрицательных коэффициентов.
