Акустические свойства сред
Акустические свойства – это физические свойства сред, которые определяют особенности генерации и распространения в данной среде упругих колебаний. Основными свойствами сред являются скорости продольных и поперечных волн, характеристический импеданс и коэффициент затухания. Скорость звука как физическая константа упругой среды достаточно подробно рассмотривалась в п. 1.5. Напомним некоторые особенности этого свойства.
Скорость звука зависит, вообще говоря, от самых разных факторов. Для газов проявляется явная зависимость от температуры, т. к. давление в газах имеет тепловую природу. Кроме того, для газов при достаточно больших градиентах давления (и/или плотности) скорость звука уже будет зависеть локально и от других параметров среды. Это имеет место при перепадах давления порядка 1 атм. Однако в случае малых (акустических) колебаний и постоянной температуры скорость звука в газах также постоянна. В твердых телах скорость звука является константой среды в широком температурном диапазоне. Это же относится и к механически нагруженным объектам – скорость звука постоянна в широком диапазоне нагрузок.
Упругие свойства изотропных твердых тел характеризуются двумя независимыми константами - модулем Юнга E и модулем сдвига G. Значениями этих модулей однозначно определяют скорости продольных cl и поперечных ct волн в безграничной среде. Отношения скоростей продольных и поперечных, а также других типов волн зависит от величины коэффициента Пуассона для данной среды (рис 1.2).
Таким образом, зная упругие модули и коэффициент Пуассона, на основе значений скоростей продольных и поперечных волн, можно вычислить скорости распространения всех других типов волн. Для всех металлов при комнатной температуре значение коэффициента Пуассона близко к 0.3. В этом случае отношение скоростей (см. также рис. 1.2):
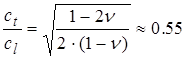
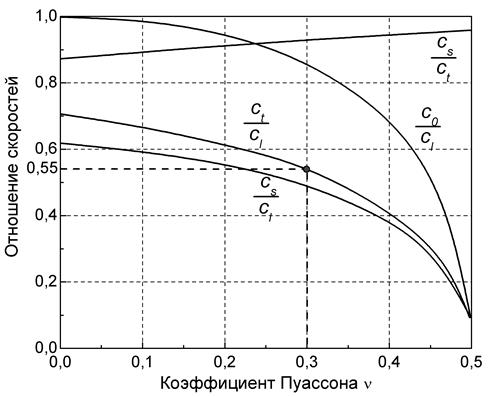 |
| Рис. 1.2. Зависимость соотношения скоростей продольных cl, поперечных ct, поверхностных cs и симметричных волн в стержне c0 от коэффициента Пуассона. |
В результате получается упрощенная формула, которую удобно применять в практике акустического контроля для металлов:
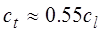 (1.45)
(1.45)
Импеданс.Важным параметром среды распространения упругих колебаний является акустический импеданс или удельное волновое сопротивление. Акустическим импедансом называют комплексное отношение звукового давления к колебательной скорости для любой волны:
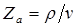 . (1.46)
. (1.46)
В отсутствие потерь акустический импеданс – действительная величина. Комплексный характер импеданса учитывают только в случае сред с большими потерями, когда колебательная скорость частиц в бегущей волне имеет мнимую составляющую.
Для безграничной среды удельный акустический импеданс является действительной величиной и называется характеристическим импедансом:
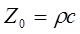 , (1.47)
, (1.47)
где 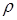 – плотность среды;
– плотность среды;
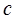 – скорость звука.
– скорость звука.
Акустический импеданс имеет размерность акустических омов:
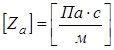 .
.
Акустический импеданс – величина комплексная. Действительная часть – активное акустическое сопротивление – связана с диссипацией энергии в системе и потерями на излучение. Мнимая часть обусловлена реакцией сил инерции и упругости в среде. Значения импеданса различны для продольной и поперечной волн. Для твердых, жидких и газообразных сред значения характеристического импеданса различаются на несколько порядков: 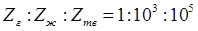 .
.
Эта особенность приводит к тому, что полые дефекты в твердом теле при помощи ультразвука выявляются с гораздо большей эффективностью, чем заполненные (например, поры, заполненные шлаком).
Затухание.При распространении волн в реальных средах происходит уменьшение амплитуды колебаний частиц в волне, что может быть вызвано расхождением лучей (дифракционным ослаблением), характерным для сферических и цилиндрических волн, а также затуханием волн в среде. Подчеркнем, что при затухании уменьшаются амплитуда и интенсивность всех типов волн, включая плоские волны.
Основная причина затухания – наличие внутреннего трения в среде. Таким образом, затухание – акустическое свойство среды, в отличие от дифракционного ослабления, которое является свойством волны. Затухание можно учесть введением дополнительного экспоненциального множителя в выражение для конкретного вида волн:
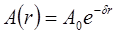 , (1.48)
, (1.48)
где 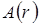 – амплитуда в точке измерения;
– амплитуда в точке измерения;
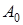 – амплитуда волны в начальный момент времени;
– амплитуда волны в начальный момент времени;
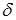 – коэффициент затухания;
– коэффициент затухания;
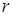 – расстояние, проходимое волной.
– расстояние, проходимое волной.
Коэффициент затухания 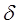 имеет размерность обратной длины (1/м), либо выражается в неперах на метр (Нп/м) и децибелах на метр (дБ/м). При этом необходимо помнить, что 1 Нп/м = 8,686 дБ/м. Коэффициент
имеет размерность обратной длины (1/м), либо выражается в неперах на метр (Нп/м) и децибелах на метр (дБ/м). При этом необходимо помнить, что 1 Нп/м = 8,686 дБ/м. Коэффициент 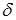 определяется как величина, обратная расстоянию, на котором амплитуда волны уменьшается в
определяется как величина, обратная расстоянию, на котором амплитуда волны уменьшается в 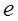 раз. Аналогичное выражение можно записать и для интенсивности волны:
раз. Аналогичное выражение можно записать и для интенсивности волны:
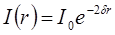 , (1.49)
, (1.49)
где 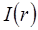 – интенсивность волны в произвольной точке среды.
– интенсивность волны в произвольной точке среды.
Коэффициент затухания представляет собой сумму коэффициентов поглощения и рассеяния:
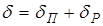 , (1.50)
, (1.50)
где 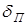 – коэффициент поглощения;
– коэффициент поглощения;
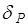 – коэффициент рассеяния.
– коэффициент рассеяния.
При рассеянии энергия не трансформируется, однако уходит из направленно распространяющейся волны в результате трансформации и многократных отражений. При поглощении звуковая энергия переходит в тепловую.
Затухание в жидкостях и газах.В гомогенных газах и жидкостях рассеяние отсутствует, и затухание определяется только поглощением. При поглощении звуковая энергия переходит в тепловую, что, в свою очередь, обусловлено двумя причинами – внутренним трением (вязкостный эффект) и эффектами теплопроводности среды. Коэффициент поглощения 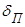 в газах может быть представлен в виде суммы вязкостного
в газах может быть представлен в виде суммы вязкостного 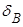 и теплового
и теплового 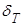 членов:
членов:
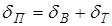 . (1.51)
. (1.51)
Коэффициент поглощения для жидкостей определяется следующим соотношением:
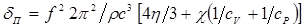 , (1.52)
, (1.52)
где 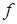 – частота;
– частота; 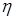 – коэффициент вязкости;
– коэффициент вязкости;
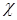 – коэффициент теплопроводности.
– коэффициент теплопроводности.
В жидкостях поглощение происходит в основном за счет внутреннего трения, поэтому 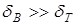 . В газах поглощение за счет трения и за счет эффектов теплопроводности в среде приблизительно совпадают, поэтому
. В газах поглощение за счет трения и за счет эффектов теплопроводности в среде приблизительно совпадают, поэтому 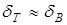 . При постоянной температуре
. При постоянной температуре 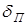 определяется только частотой
определяется только частотой 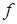 . Для гомогенных газов и жидкостей коэффициент поглощения пропорционален квадрату частоты. В этих случаях вводят коэффициент
. Для гомогенных газов и жидкостей коэффициент поглощения пропорционален квадрату частоты. В этих случаях вводят коэффициент 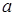 , характеризующий поглощение в среде:
, характеризующий поглощение в среде:
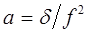 . (1.53)
. (1.53)
Учитывая, что поглощение обусловлено вязкостью среды и эффектами теплопроводности, можно представить коэффициент 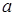 суммой двух составляющих:
суммой двух составляющих:
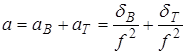 . (1.54)
. (1.54)
Значения этих коэффициентов для воды и воздуха приведены в табл. 2.
Таблица 2
