Оценивание параметров моделей с коррелированными возмущениями

Если имеется автокорреляция возмущений, то для оценки параметров модели используют другой частный случай обобщенного метода наименьших квадратов. Пусть по временным рядам переменных X и Y строится парная линейная модель

(t=1, 2, …, n),

(33)

уравнение регрессии которой имеет вид:

(t=1, 2, …, n),

(34)

где b₀, b₁ — оценки параметров b₀ и b₁ соответственно.

Первоначально исходные переменные и свободный член b₀ уравнения регрессии преобразуются с помощью формул:

	;	(35)
	;	(36)
	(t=2, 3, …, n),	(37)

где r₍₁₎ — коэффициент автокорреляции остатков первого порядка [см. формулу (21)].

В результате уравнение (34) трансформируется в уравнение

(t=2, 3, …, n),

(38)

параметры которого определяются обычным МНК. После этого рассчитывается свободный член b₀ исходного уравнения (34) по формуле

.

(39)

Пример 2

Исследуется зависимость цены акции предприятия (переменная Y, руб.) от индекса фондового рынка (переменная X, пунктов) по данным за 12 месяцев. Имеются временные ряды средневзвешенных за месяц значений переменных:

Месяц	1	2	3	4	5	6	7	8	9	10	11	12
X	244	222	201	186	215	248	256	255	217	224	263	292
Y	152	154	149	136	139	148	152	156	152	156	169	176

Требуется:

1. Построить линейную модель парной регрессии Y по X.

2. Проверить наличие автокорреляции возмущений модели методом Дарбина-Уотсона.

3. При обнаружении автокорреляции возмущений построить обобщенную модель регрессии.

Решение

1. По временным рядам переменных строим модель парной регрессии

(t=1, 2, …, n; n=12),

параметры которой оцениваем обычным методом наименьших квадратов. С помощь табличного процессора MS Excel были определены коэффициенты уравнения регрессии : b₀=81,8; b₁=0,304. Уравнение регрессии, таким образом, имеет вид:

.

Уравнение регрессии статистически значимо на уровне a=0,05: коэффициент детерминации имеет значение R²=0,671; F-статистика — F=20,41; табличное значение F-критерия Фишера — F_{0,05; 1;10}=4,96.

Значение углового коэффициента уравнения b₁=0,304 показывает, что при росте индекса рынка на 1 пункт цена акции возрастает в среднем на 0,304 руб., т. е. на 30,4 коп.

График зависимости Y от X выглядит следующим образом:

2. Построим график временного ряда остатков регрессии и проведем его визуальный анализ. Предсказываемые уравнением регрессии значения результата и остатков (t=1, 2, …, n; n=12) приведены в таблице:

t	1	2	3	4	5	6	7	8	9	10	11	12
xt	244	222	201	186	215	248	256	255	217	224	263	292
yt	152	154	149	136	139	148	152	156	152	156	169	176
	156	149	143	138	147	157	160	159	148	150	162	170
et	-3,9	4,8	6,2	-2,3	-8,1	-9,1	-7,6	-3,2	4,3	6,2	7,3	5,5

График временного ряда остатков имеет вид:

Визуальный анализ графика указывает на положительную автокорреляцию возмущений: видно, что на графике имеются чередующиеся зоны положительных и отрицательных остатков регрессии. Проверим это предположение методом Дарбина-Уотсона. Определяем d-статистику по формуле

.

Критические значения d-критерия для числа наблюдений n=12 и уровня значимости a=0,05 составляют d₁=0,97 и d₂=1,33 (см. приложение). Так как 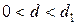, то это свидетельствует о наличии положительной автокорреляции возмущений. На это же указывает и коэффициент автокорреляции остатков первого порядка

,

который превышает критическое значение 0,346 для n=12 и a=0,05 (см. приложение).

3. Применим обобщенный метод наименьших квадратов для оценки параметров исходной модели, для чего преобразуем исходные данные по формулам:

	;
	(t=1, 2, …, n; n=12).

Преобразованные данные имеют вид:

t	1	2	3	4	5	6	7	8	9	10	11	12
	—	65,7	58,8	57,3	95,9	110,3	97,2	91,0	53,7	85,0	119,5	123,6
	—	56,7	50,4	40,6	51,9	59,0	57,2	58,7	52,1	58,7	69,1	67,8

Обычным методом наименьших квадратов определяем коэффициенты преобразованного уравнения регрессии (t=1, 2, …, n; n=12): ; . Свободный член исходного уравнения

.

Окончательно исходное уравнение регрессии примет вид:

.

Данное уравнение статистически значимо на уровне a=0,05: коэффициент детерминации имеет значение R²=0,666; F-статистика — F=17,92; табличное значение F-критерия Фишера — F_{0,05; 1;9}=5,12.

Таким образом при росте индекса рынка на 1 пункт цена акции возрастает в среднем на 0,257 руб. или на 25,7 коп.

ЛИТЕРАТУРА

1. Балдин К.В., Быстров О.Ф., Соколов М.М.Эконометрика: Учеб. пособие для вузов. — М.: ЮНИТИ–ДАНА, 2004. — 254 с.

2. Доугерти К.Введение в эконометрику.—М.: ИНФРА-М, 1997. —402 с.

3. Дрейпер Н, Смит Г.Прикладной регрессионный анализ. — М.: Статистика, 1973. — 392 с.

4. Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов / Под ред. проф. Н.Ш. Кремера. — М.: ЮНИТИ-ДАНА, 2002. — 311 с.

5. Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. — М.: Финансы и статистика, 2002. — 192 с.

6. Эконометрика: Методические указания по изучению дисциплины и выполнению контрольной и аудиторной работы на ПЭВМ для студентов III курса по специальностям «Финансы и кредит», «Бухгалтерский учет, анализ и аудит», «Экономика труда» . — М.: Вузовский учебник, 2005. — 122 с.

7. Эконометрика: Учебник / Под ред. И.И. Елисеевой. — М.: Финансы и статистика, 2002. — 344 с.