Формирование уравнений для определения напряжений ветвей базы и токов ветвей кобазы.

1. Неособые ветви базы и кобазы

В₂^Н = {4}: u₂ = E₂(t)

В₃^Н = {3}: u₃ = u₃(t)

В₆*^Н = {10}: i₁₀ = J₁₀(t)

В₅*^Н = {12,13}: i₁₂ = i₁₂(t) i₁₃ = i₁₃(t)

В₄*^Н = {8}:

2. Особые ветви базы и кобазы

Так как число элементов множеств В₄^О и В₄*^Н одинаково, то следует сформировать систему уравнений для определения напряжений особых ветвей базы R-типа

Ψ\ Ψ₄ = {4,3,1,2,5,8,9,11,12,13,10}\{1,2,5,8} = {4,3,9,11,12,13,10}

В₄^О = {2,3}

Уравнение для а_к = 1

Левая часть уравнения:

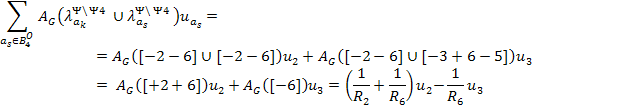
Правая часть уравнения:

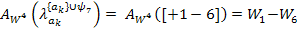
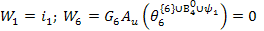
Полученное уравнение:

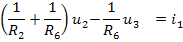
Уравнение для а_к = 3

Левая часть уравнения:

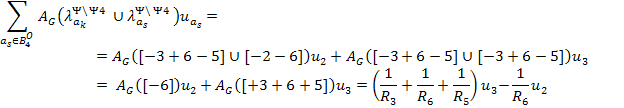
Правая часть уравнения:

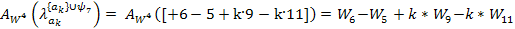
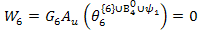
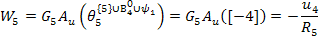
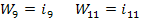
Полученное уравнение

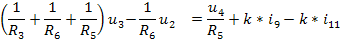
Токи особых ветвей кобазы R-типа:

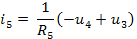
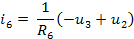
Формирование системы уравнений для особых ветвей L-типа:

Ψ\ Ψ₅ = {1,2,3,4,5,6,9,10,11,12,13,14}\{9,10,11,13,14} = {1,2,3,4,5,6, 12}

В₅^О = {10,13}

Уравнение для а_к = 10

Левая часть уравнения:

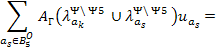
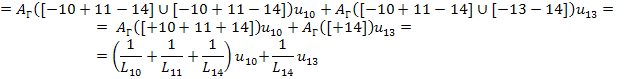
Правая часть уравнения:

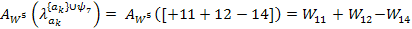
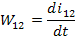
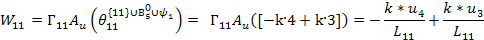
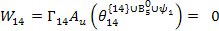
Полученное уравнение:

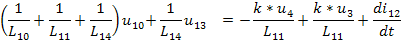
Уравнение для а_к = 13

Левая часть уравнения:

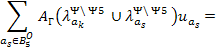
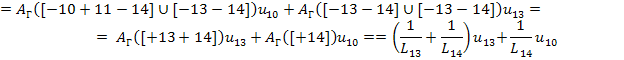
Правая часть уравнения:

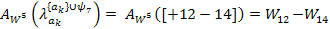
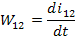
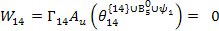
Полученное уравнение:

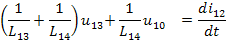
Формирование уравнений для определения токов ветвей базы и напряжений ветвей кобазы

Токи ветвей базы: В = {4,2,3,10,13}

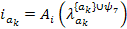
Λ = [-4+5-k·9+k·11][-2+1-6][-3+6-5+k·9-k·11][-10+11+12-14][-13+12-14]

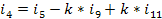
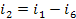
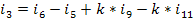
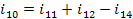
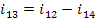
Напряжения ветвей кобазы: В* = {5,6,9,11,14,1,12}

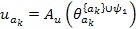
Θ = [-5-4+3][-6+2-3][-9+k·4-k·3][-11-k·4+k·3-10][-14+10+13][-1-2][-12-10-13]

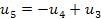
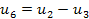
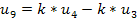
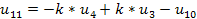
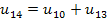
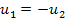
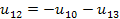
Формирование дифференциальных уравнений

B∩ Ψ₃ = {4}

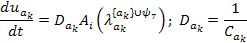
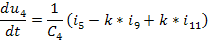
B*∩ Ψ₅ = {9,11,14}

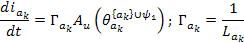
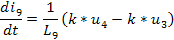
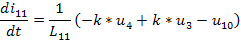
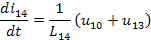
10. Полученные уравнения:

i₁ = J₁

i₁₂ = J₁₂

u₄ = u₄(t)

i₉ = i₉(t)

i₁₁ = i₁₁(t)

i₁₄ = i₁₄(t)

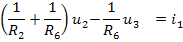
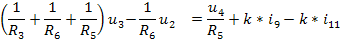
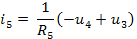
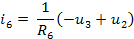
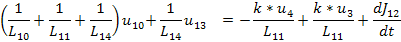
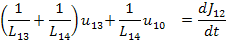
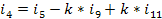
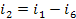
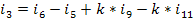
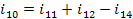
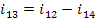
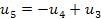
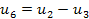
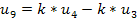
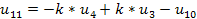
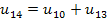
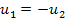
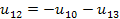
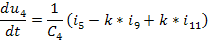
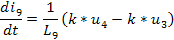
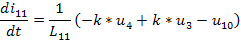
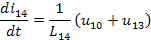
Уравнения переходного процесса, полученные в программе РИТМ

----------------------------------------------------------------------------

w(1-1) = i(1-1)

w(9-1) = i(9-1)

w(11-1) = i(11-1)

w(6-1) = 0

w(5-1) = [-u(4-1)] / R(5-1)

[1/R(2-1)+1/R(6-1)]*u(2-1) + [-1/R(6-1)]*u(3-1) = w(1-1)-w(6-1)

[-1/R(6-1)]*u(2-1) + [1/R(3-1)+1/R(5-1)+1/R(6-1)]*u(3-1) = -w(5-1)+w(6-1)+2.

00000*w(9-1)-2.00000*w(11-1)

----------------------------------------------------------------------------

i(5-1) = [u(3-1)-u(4-1)] / R(5-1)

i(6-1) = [u(2-1)-u(3-1)] / R(6-1)

----------------------------------------------------------------------------

w(12-1) = dJ(12-1)/dt

w(11-1) = [2.00000*u(3-1)-2.00000*u(4-1)] / L(11-1)

w(14-1) = 0

[1/L(10-1)+1/L(11-1)+1/L(14-1)]*u(10-1) + 1/L(14-1)*u(13-1) = w(11-1)+w(12-1

)-w(14-1)

1/L(14-1)*u(10-1) + [1/L(13-1)+1/L(14-1)]*u(13-1) = w(12-1)-w(14-1)

----------------------------------------------------------------------------

u(1-1) = -u(2-1)

u(5-1) = u(3-1)-u(4-1)

u(6-1) = u(2-1)-u(3-1)

u(9-1) = -2.00000*u(3-1)+2.00000*u(4-1)

u(11-1) = 2.00000*u(3-1)-2.00000*u(4-1)-u(10-1)

u(12-1) = -u(10-1)-u(13-1)

u(14-1) = u(10-1)+u(13-1)

----------------------------------------------------------------------------

i(2-1) = i(1-1)-i(6-1)

i(3-1) = -i(5-1)+i(6-1)+2.00000*i(9-1)-2.00000*i(11-1)

i(4-1) = i(5-1)-2.00000*i(9-1)+2.00000*i(11-1)

i(10-1) = i(11-1)+i(12-1)-i(14-1)

i(13-1) = i(12-1)-i(14-1)

----------------------------------------------------------------------------

du(4-1)/dt = [i(5-1)-2.00000*i(9-1)+2.00000*i(11-1)] / C(4-1)

----------------------------------------------------------------------------

di(9-1)/dt = [-2.00000*u(3-1)+2.00000*u(4-1)] / L(9-1)

di(11-1)/dt = [2.00000*u(3-1)-2.00000*u(4-1)-u(10-1)] / L(11-1)

di(14-1)/dt = [u(10-1)+u(13-1)] / L(14-1)

----------------------------------------------------------------------------

12. Опыт трёхфазного короткого замыкания

Расчётная схема:

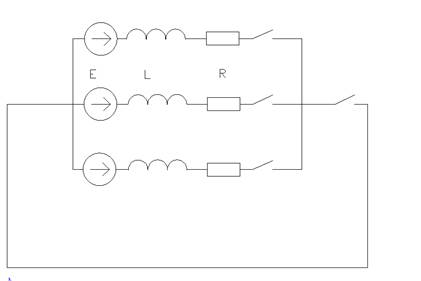
Исходные данные:

Uн = 110 кВ; Sкз = 2500 МВА; f = 50 Гц; r = 0.1x; t_к = 0.04 с

Расчёт параметров цепи:

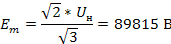
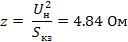
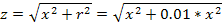
Отсюда х = 4.82 Ом и r = 0.44 Ом

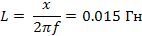
Моделирование процесса в программе РИТМ:

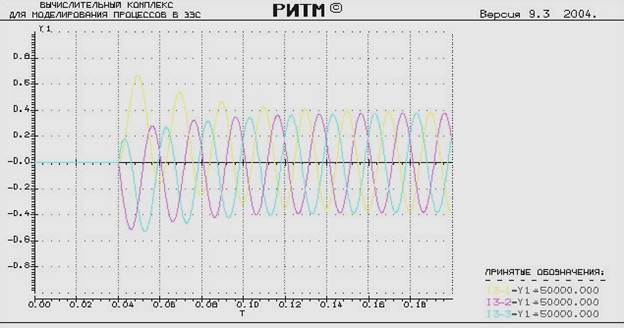
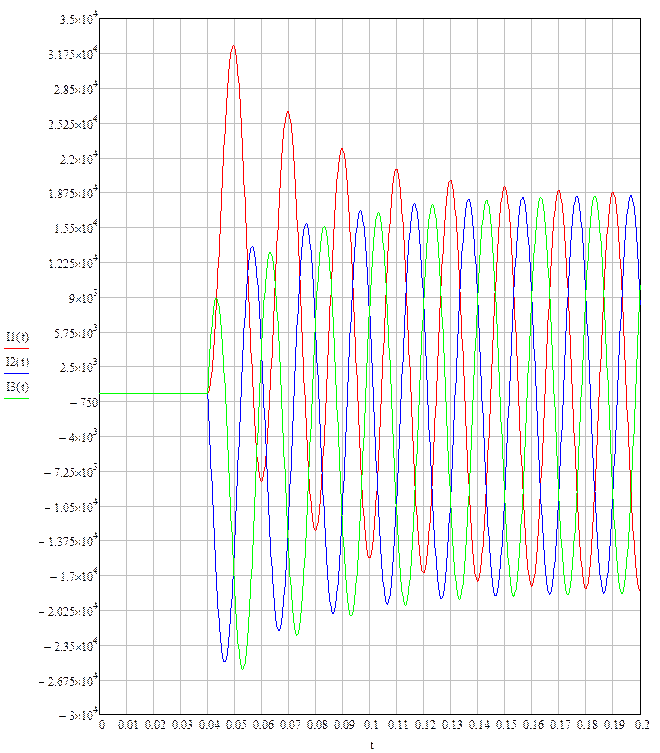
Максимальное значение ударного тока: i_1уд = 33052 A

Амплитуда тока в установившемся режиме: I_1m = 18671 А

Ударный коэффициент: К_у = i_1уд / I_1m = 1.77

Расчёт процесса в программе MathCad:

Исходные данные:

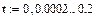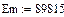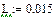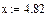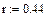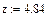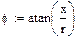Переходный процесс при замыкании ключей в каждой фазе описываются дифференциальным уравнением:

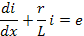
Решение данного неоднородного дифференциального уравнения есть сумма частного решения неоднородного дифференциального уравнения (установившееся значение тока i’’) и общего решения соответствующего ему однородного (с нулевой правой частью) дифференциального уравнения (апериодическая составляющая тока), которое имеет вид:

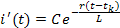
Начальные условия: i(t_k) = i’+i’’= 0, отсюда С = -i’’(t_k)

Установившиеся значения фазных токов:

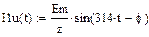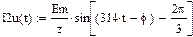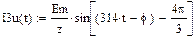Апериодические составляющие фазных токов:

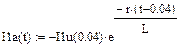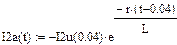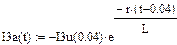Графики i(t):

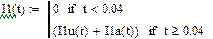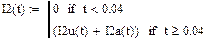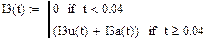Данные из графика:

Максимальное значение ударного тока: i_1уд = 32492 A

Амплитуда тока в установившемся режиме:

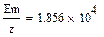Ударный коэффициент: К_у = i_1уд / I_1m = 1.75

Графики i(t)