Получение требуемого сплава

Предприятию требуется изготовить некоторое количество сплава, содержащего не менее 15 компонент олова, 55 компонент цинка и 30 компонент свинца. Требуемый сплав изготавливается из трех исходных сплавов, в которых содержатся вышеуказанные составляющие. Данные о содержании олова, цинка и свинца в исходных материалах приведены в таблице, там же задана стоимость единицы каждого сплава.

Следует определить, какие из исходных сплавов и в каких количествах нужно использовать для получения требуемого сплава, чтобы суммарные затраты на исходные сплавы были минимальными.

Составляющие	Кол-во компонент составляющих в исходных материалах	Необходимое кол-во компонент в сплаве
	Сплав1	Сплав2	Сплав3
Свинец
Цинк
Олово
Цена единицы материала (руб.)

Математическая модель задачи выглядит следующим образом.

Целевая функция имеет вид:

5× x₁+4× x₂+7× x_3® min,

Ограничения имеют вид:

40× x₁+30× x₂+25× x₃=30

40× x₁+60× x₂+45× x₃=55

20× x₁+10× x₂+30× x₃=15

x_j³ 0, j= .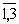

Вид электронной таблицы Excel, созданной для решения задачи, представлен на рис. 19.

Поясним содержание некоторых ячеек таблицы.

В блоке ячеек В3:D3 находятся искомые значения x_j, которые до выполнения поиска решения были равны 0. Адрес данного блока входит в поле ввода Изменяя ячейки в окне “Поиск решения” (см. рис. 21). Ячейки блока выполняют роль переменных целевой функции и ограничений- x_j.

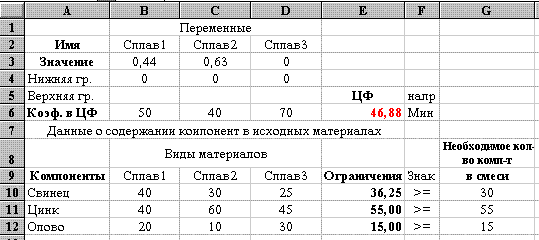
Рис. 19

Блок ячеек B4:D4 содержит правые части граничных неравенств (граничных условий). В ячейках блока содержатся нулевые значения (см. рис. 19).

Блок ячеек B6:D6 содержит данные о цене единицы исходных материалов, каждая его ячейка играет роль коэффициента при целевой функции в математической модели.

В блоках ячеек B10:D12 и G10:G12 находятся данные, соответствующие коэффициентам a_ij и b_i ограничений математической модели.

Рис. 20

Сами формулы целевой функции и ограничений расположены соответственно в ячейке E6 и ячейках E10, E11, E12 (см. рис. 19 и 20). Вид электронной таблицы в режиме отображения формул представлен на рис. 20.

После ввода условий задачи необходимо перейти к поиску решения, инициировав соответствующее диалоговое окно (см. рис. 21). Данные в окно удобно вводить с помощью мыши. Для этого необходимо установить курсор в соответствующее поле ввода, затем выделить на рабочем листе требуемые ячейки, адреса выбираемых ячеек автоматически будут появляться в поле ввода.

Обычно в поле ввода Изменяя ячейки (см. рис. 21) заносятся адреса ячеек, которые выполняют роль переменных математической модели. Таким образом, под x₁, x₂, x₃ отводятся ячейки B3, C3, D3.

Ограничения удобно задавать поблочно. Первое ограничение данного примера (см. рис. 21) представляет собой запись граничных условий, в которой каждая ячейка левого блока больше либо равна каждой ячейке правого блока. Левый блок означает, как известно, совокупность переменных x_j, правый- множество нижних границ переменных. В данном примере нижней границей всех x_j является 0, поэтому можно было бы записать: $B$3:$D$3>=0. Вторая запись в группе Ограничения представляет три ограничения по содержанию требуемых компонентов в сплаве. В каждой ячейке левого блока содержится формула одного из ограничений (см. рис. 20), ячейки правого блока содержат требования b_i. По-прежнему, знак “>=“ относится каждой ячейке обоих блоков.

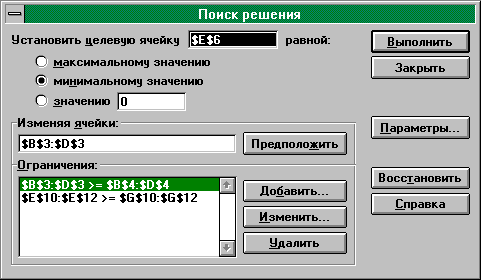
Рис. 21

Способ задания ограничений поблочно существенно облегчает ввод однотипных ограничений. Так, для данного примера двумя записями были заданы шесть ограничений.

Результаты поиска решения заносятся в ячейки таблицы (см. рис. 19). Прежде всего это значения x_j. Для получения требуемого сплава нужно 0,44 единицы сплава1 и 0,63 единиц сплава2. Стоимость нового сплава равна 46,88 д. е., количество компонент свинца, цинка и олова равно соответственно 36,25; 55; 15 компонент.

Транспортная задача

Три поставщика одного и того же продукта располагают в планируемый период следующими запасами этого продукта: первый- 120 условных единиц, второй- 100 и третий 80 единиц. Этот продукт должен быть перевезен к трем потребителям, спросы которых соответственно равны 90, 90 и 120 условных единиц. Приведенная ниже таблица содержит показатели затрат, связанных с перевозкой продукта из i-го пункта отправления в j-й пункт потребления.

Требуется перевезти продукт с минимальными затратами.

Поставщики	Потребители и их спрос	Запасы
	А	Б	В
I
II
III
Спрос

Математическая модель задачи выглядит следующим образом.

Целевая функция имеет вид:

7× x₁₁+6× x₁₂+4× x₁₃+3× x₂₁+8× x₂₂+5× x₂₃+2× x₃₁+3× x₃₂+7× x_33® min,

Ограничения имеют вид:

x₁₁+x₁₂+x₁₃=120,

x₂₁+x₂₂+x₂₃=100,

x₃₁+x₃₂+x₃₃=80,

x₁₁+x₂₁+x₃₁=90,

x₁₂+x₂₂+x₃₂=90,

x₁₃+x₂₃+x₃₃=120,

x_ij³ 0, i, j= .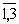

Вид электронной таблицы Excel, созданной для решения задачи, представлен на рис. 22

Искомые значения x_ij находятся в блоке ячеек B4:D6. Адрес данного блока входит в поле ввода Изменяя ячейки в окне “Поиск решения” (см. рис. 24). Требования к ограничениям по спросу и запасам представлены соответственно в ячейках B7:D7 и E4:E6. Коэффициенты ЦФ, означающие затраты на доставку расположены в блоке ячеек B12:D14.

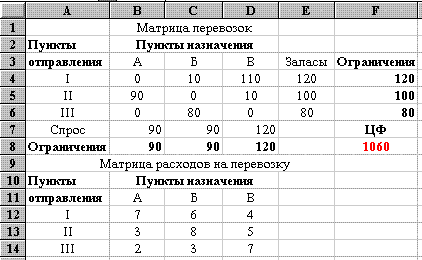
Рис. 22

Формулы целевой функции и ограничений находятся соответственно в ячейке F8 и ячейках B8:D8 (ограничения по спросу), F4:F6 (ограничения по запасам) (см. рис. 22 и 23). Вид электронной таблицы в режиме отображения формул представлен на рис. 23.

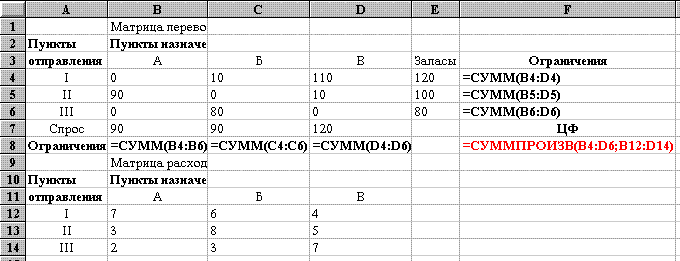
Рис. 23

Первая запись в группе Ограничения (см. рис. 24) представляет ограничения по нижней границе x_ij. Вторая и третья записи выражают ограничения по уровню спроса и запасов соответственно.

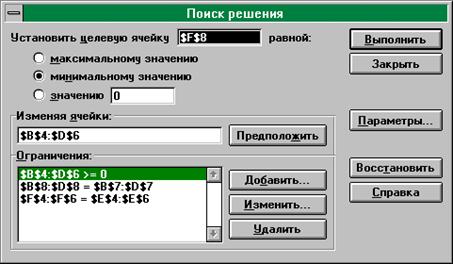
Рис. 24

Результаты поиска решения представлены на рис. 22.