Модель идеального перемешивания

На рис.4.1.1 представлена схема аппарата идеального перемешивания

Аппарат идеального смешения характеризуется тем, что интенсивность перемешивания в нем настолько велика, что поступающее с потоком вещество мгновенно распространяется по всему объему аппарата и появляется в выходном потоке. Таким образом, в таком аппарате любое возмущение на входе мгновенно появляется на выходе. Составим для такого аппарата уравнение материального баланса при следующих условиях:

1. Объемный расход жидкости постоянный.

2. Объем жидкости в аппарате постоянный.

3. Концентрация индикаторного вещества (трассера) на выходе из аппарата равна концентрации его в аппарате. (условия идеального смешения.

4. В аппарате соблюдаются условия квазистационарности – изменение концентрации во входном потоке происходит медленнее, чем устанавливается равномерное распределение вещества по всему объему.

Составим уравнение материального баланса вещества для этого аппарата.

Входной поток вещества будет равен

J_М,вх(t)=v×c_вх(t)× (4.1.1)

Выходной поток вещества будет равен:

J_М,вых(t)=v×c_вых(t)× (4.1.2.)

Накопление вещества в аппарате за время от 0 до t, будет равно

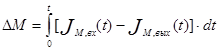(4.1.3)

Продифференцируем уравнение (3.1.3) по времени с учетом того, что масса вещества в аппарате будет равна произведению концентрации на объем аппарата и используем для потоков выражения (3.1.1) и (3.1.2):

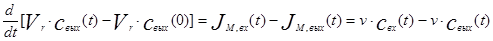(4.1.4)

Где V_r – объем аппарата в м³.

Учитывая, что в начальный момент времени концентрации в аппарате была постоянной величиной, разделим обе части уравнения (3.1.4) на объемный расход смеси v и перенесем второе слагаемое правой части в левую часть. В итоге получим следующее уравнение:

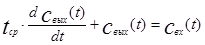(4.1.5)

Где 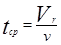- среднее время пребывания смеси в аппарате, [cек.], t-текущее время, [cек].

Полученное дифференциальное уравнение (4.1.5) представляет собой математическую модель аппарата идеального перемешивания. Для того чтобы узнать, как изменяется с_вых(t), необходимо решить уравнение (4.1.5) при заданной функции с_вх(t) (внешнее воздействие).

В качестве типовых внешних воздействий при анализе поведения объектов чаще всего используют следующие виды воздействий:

· Ступенчатое воздействие с_вх(t)= А=const

· Импульсное воздействие с_вх(t)=d(е)-функция Дирака.

· Синусоидальное воздействие с_вх(t)=C₀ sin(wt)

Рассмотрим решение уравнения (3.1.5) при ступенчатом входном воздействии. Тогда уравнение (3.1.5) принимает вид:

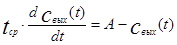(4.1.6)

Уравнение ( 4.1.6) можно решить разделением переменных. Для этого разделим обе части уравнения (4.1.6) на величину времени контакта t_ср и произведем операцию разделения переменных. В результате получим уравнение в полных дифференциалах:

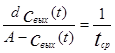(4.1.7)

После интегрирования уравнения (4.1.7) получаем:

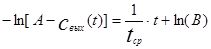(4.1.8)

Где В – постоянная интегрирования, которая может быть определена из начальных условий: при t=0 c_вых(t) = 0. Отсюда получаем, что -ln(A)=ln(B).

Подставляя найденное значение произвольной постоянной в уравнение (4.1.8), получим:

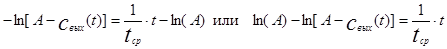(4.1.9)

После потенцирования окончательно получим

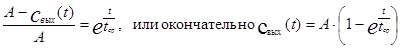(4.1.10)

На рис.4.1.2 представлен график изменения выходной концентрации при воздействии на вход единичного ступенчатого возмущения. Если в уравнении

(4.1.10) принять t=t_ср, тогда получим:

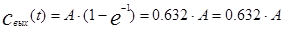(4.1.11)

Полученное значение свидетельствует о том, что среднее время пребывания в аппарате идеального перемешивания есть время, в течение которого выходной параметр с_вых(t) изменится на 63.25% от величины нанесенного на объект возмущения..

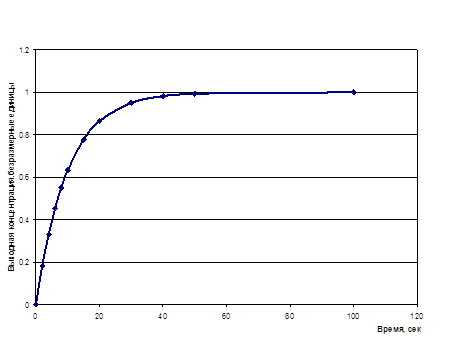
Рис.4.1.2 . Кривая разгона аппарата идеального перемешивания на ступенчатое единичное возмущение входа.

Среднее время пребывания t_ср является параметром модели аппарата идеального перемешивания, Модель аппарат идеального перемешивания применяется для аппаратов, у которых обеспечиваются условия интенсивного перемешивания и время смешения много меньше среднего времени пребывания вещества в аппарате. Cреднее время пребывания может быть определено из экспериментально полученной кривой разгона следующим образом. Если прологарифмировать уравнение (3.10) ( его первую часть) мы получим уравнение

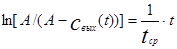
Это уравнение представляет собой уравнение прямой в координатах

ln[A/(A-c_вых(t))] – t. При этом тангенс угла наклона этой прямой есть величина, обратная времени пребывания. На следующем рисунке представлена графическая зависимость для определения среднего времени пребывания по экспериментальной кривой разгона.

Рис.3.1.3. Определение времени пребывания по кривой разгона.