Основы теории вероятности

Суммой событий А_i называется событие С состоящее в появлении события А или события В или их обоих вместе.

Суммой события А и В называется событие С заключенное в выполнении хотя бы одного из названых событий.

Произведением нескольких событий называется событие заключающееся в совместном выполнении всех этих событий.

Теорема умножения вероятностей.

Событие А называется зависимым от события В если его вероятность меняется в зависимости от того произошло событие В или нет.

Для независимых событий условная и безусловная вероятность совпадают.

Вероятность появления двух зависимых событий равна произведению вероятностей одного из них на вероятность другого вычисленную при условии, что первое событие имело место.

Р(А*В)=Р(А)*Р(В/А)=Р(В)*Р(В/А)

Вероятность произведения нескольких событий равна произведению вероятностей этих событий причем вероятность каждого следующего события вычисляется при условии, что все предыдущие имели место.

Р(А₁;А₂…А_n)=Р(А₁)*Р(А₂/А₁)*…

*Р(А_n/А₁,А₂…А_n-1)

Теорема сложения вероятностей совместных событий

Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.

Р(А)+Р(В)=Р(А)+Р(В)-Р(А*В)

Вероятность появления хотя бы одного события

Вероятность появления события А заключающееся в наступлении хотя бы одного из независимых совокупностей событий .А₁,А₂…А_n равна разности между единицей и произведением вероятности противоположных событий А₁,А₂…А_n

Р(А)=1-q¹*q²*…*qⁿ

Формула полной вероятности

Пусть событие А может появиться вместе с одним из образующих полную группу попарнонесовместных событий Н₁,Н₂…Н_n называемых гипотезами, тогда вероятность события А вычисляется как сумма произведений вероятностей каждой гипотезы на вероятность события А при этой гипотезе

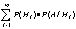
Формула Бейса

Пусть имеется полная группа попарнонесовместных гипотез Н₁,Н₂…Н_n с известными вероятностями появления. В результате проведения опыта появилось некоторое события А, требуется переоценить вероятности гипотез при условии, что событие А произошло

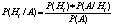
Повторение опытов

Несколько опытов называются независимыми, если вероятность одного или иного из исходов каждого их опытов не зависит от того какие исходы имели другие опыты.

Теорема.Если производится n независимых опытов в каждом из которых событие А появляется с одинаковой вероятностью р, причем то тогда вероятность того, что событие А появится ровно m раз определяется по формуле.

Формула Бернули

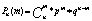
формула Бернули применяется в тех случаях, когда число опытов невелико, а вероятности появления достаточно велики.

Если число испытаний n стремится к 0, а вероятность появления события А в каждом из опытов р стремится к 0, то для определения вероятности появления события А ровно m раз применяютформулу Пуассона

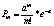a=n*p

Если число опытов достаточно велико но не бесконечно, а вероятность появления события А в каждом опыте не стремится к 0, применяют локальную и интегральную теоремы Лапласа

Локальная теорема Лапласа.Вероятность того, что в n независимых испытаниях в каждом из которых вероятность появления события А равно р причем 1>р>0, то это событие наступает ровно m раз приблизительно равна

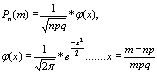
Интегральная теорема Лапласа. Вероятность того, что в n независимых испытаниях в каждом из которых вероятность появления события А равно р, причем 1>р>0, то событие А наступит не менее m₁ раз и не более m₂ разаприблизительно равно