Формулы дифференцирования

1. (f(h(x))) ' = f' (h(x)) x ∙ h'(x)

2. (sin x) ' = cos x

3. (cos x) ' = - sin x

4. (tg x) ' = 1/cos² x

5. (ctg x) ' = 1/sin ² x

6. (a^x) ' = a^x ∙ ln a

7. (е^x) ' = е^x

8. (ln x) ' = 1/x

9. (log_a x) ' = 1/ x ∙ ln_aа

10. (arcsin x) ' = 1/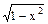

11. (arccos x) ' = -1/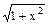

12. (arctg x) ' = 1/ 1+x²

13. (arcctg x) ' = -1/1+x²

Пример. Вычислите производную

y = sin ³ (1-x²)

y'= (sin³ (1-x²))'* (sin (1-x²))'* (1-x²)' = 3 sin² (1-x² ) * cos (1-x² ) * (-2x) =

= -6x * sin²(1-x²) * cos (1-x²)

Определение. Пусть функция y = f(x), x Є(a;b) дифференцируема в некоторой точке x_o Є(a;b), т.е. в точке x_o существует предел lim Δf(x_o) / Δx = f'’ (x_o)

Δ^{x → 0}

Отсюда имеем Δ f(x_o) / Δx = f’(x_o) + α , где α - величина бесконечно малая при Δ x→0, т.е. lim α = 0

Δ ^{x → 0}

Значит Δ f(x_o) = f'' (x_o) ∙ Δx + α∙ Δx.

Второе слагаемое бесконечно малое при Δx→0, поэтому d f(x_o )= f ' (x_o )∙ Δx или

dy = y'∙Δ x.

Пример. Вычислите дифференциал функции y = x² + cos 3x - 5

Dy = (x² + cos 3x – 5)'dx = (2x – 3 sin 3x) dx.

Определение. Дифференциальная функция f(x) , определенная на некотором промежутке x, называется первообразной для функции f(x), определенной на том же промежутке, если для всех x из этого промежутка F'(x) = f(x) или d F(x) = f(x) * dx

Определение. Совокупность всех первообразных для функции f(x), определенных на некотором промежутке x, называется неопределенным интегралом от функции f(x) на этом промежутке и обозначается символом

∫ f(x) dx = f(x) + C, где F(x) - первообразная

C– производная постоянная.

Для вычисления неопределенного интеграла существует таблица основных интегралов (см.учебник Математика для техникумов И.И.Валуцэ), стр.251).

Пример. Найти

1. ∫(4x³ – 6x² + 2x + 3)dx = ∫4x³ dx - ∫6x² dx + ∫2xdx + ∫3dx = 4 x⁴/4 – 6 x³/3 + 2 x²/2 +

+3x + C.

2. ∫(5x⁴ – 8/cos²x + 3√x + 1) dx = ∫ 5x⁴ dx – ∫8/cos²x * dx + ∫3√x dx + ∫dx =

= 5 * x⁵/5 – 8 * tg x + 3 x^3/2/ 3/2 + x + C = x⁵ - 8 tg x + 2x√x + x + C.

3. ∫2^3x * 3^x dx = ∫(2³ * 3)^x dx = ∫ 24 ^x dx = 24^x / ln 24 + C.

Определение. Приращения F(b) – F (a) любой из первообразных функций f(x) + C при изменении аргумента от х = а до х = b называется определенным интегралом от а до b функции f(x), и обозначается 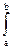f(x) dx = F(x) 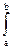= F(b) – F(a), и называется формулой Ньютона-Лейбница.

Пример. Вычислить

_{2 2}

1. ∫ (x² – 3x + 7)dx = ( 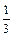x³ - 3/2 x² + 7x) | = (1/3 * 2³ – 3/2 * 2² + 7*2) – (1/3 *(-1) ³ -

^{-1 -1}

- 3/2 (-1) ² + 7*(-1)) = 19,5

Определение. Фигура ограниченная графиком функции y = f(x), отрезком [a;b] и прямыми х = а и х = b называется криволинейной трапецией.

_b

S= ∫ f(x) dx = F(b) – F(a)

^a

Пример. Вычислить площадь фигуры ограниченной y = ½ x² + 1 y = 0 x = -2 x = 3

y _{3 3}

S= ∫ (1/2 x² + 1) dx = (1/6 x³ + x) | = (1/6 * 3³+3) -

^{-2 -2}

- (1/6 (-2)³ – 2) = 10 5/6

-2 0 3 x

Тема 1.2. Обыкновенные дифференциальные уравнения

Решение различных задач методом математического моделирования сводится к отысканию неизвестной функции из уравнения, содержащего независимую переменную, искомую функцию и производные этой функции. Такое уравнение называется дифференциальным.

Определение. Решением дифференциального уравнения называется всякая функция, которая обращает данное уравнение в тождество.

Символически дифференциальное уравнение записывается так:

F(x, y, y' , y'', .....y ^(h)) = 0

2x + y – 3y'= 0 y'² – 4 = 0, sin y'= cos xy, y'' = 2x являются дифференциальными уравнениями.

Определение 2. Порядком дифференциального уравнения называются наибольший порядок производных, входящих в данное уравнение.

xy' + y – 2 = 0 – уравнение первого порядка

y'' + 7y'- 3y = 0 – уравнение третьего порядка

Определение 3. Дифференциальным уравнением первого порядка называется уравнение вида F(x, y, y') = 0

y'= f(x, y) – уравнение первого порядка, разрешенное относительно производной.

Определение 4. Всякое отдельно взятое решение дифференциального уравнения называется его частным решением.

Определение 5. Функция, заданная формулой y = (e (x,C) или y = y(x,C) – представляет общее решение дифференциального решения F(x, y, y') = 0 или

y' = f(x,y).

Задача Коши. При решении конкретных задач часто необходимо выделить из всей совокупности решений дифференциального уравнения то частное решение, которое является ответом на поставленный вопрос. Для того чтобы из всей совокупности решений выделить отдельную интегральную кривую, задают так называемые начальные условия.

В случае дифференциальных уравнений первого порядка y' = f(x, y) под начальным условием для его решения y = y(x) понимают условия, состоящие в том, что y = y_o при х = х_о т.е. y (х_о) = y_o, где x_o и y_o - заданные числа (начальные данные), такие, что при х = х_о и y = y_o функция f(x, y) имеет смысл, т.е. существует f(x_о, y_о).

Определение 6. Задача нахождения частного решения дифференциального уравнения, удовлетворяющего заданным начальным условиям, называется задачей Коши.

В случае дифференциального уравнения первого порядка задача Коши формулируется следующим образом: найти решение y = y(x) уравнения y' = f(x, y), удовлетворяющее при заданных начальных данных (x_о, y_о) начальному условию

y (х_о) = y_o, или, в другой записи, y_х=х0 = y_o , где x_о, y_о – заданные числа.

Определение 7. Дифференциальное уравнение называется уравнением с разделяющимися переменными, если имеет следующий вид: y'= f₁(x) f₂(y) или

dy/f₂(y) = f₁(x) dx.

Теорема: Если существуют интегралы ∫dy/f₂(y) и ∫ f₁(x) dx, то общий интеграл уравнения с разделенными переменными задается уравнением

F₂ (y) = F₁(x) + C, где F₂(y) и F₁(x) – некоторые первообразные соответственно функций 1/f₂ (y) и f₁ (x).

При решении дифференциальных уравнения с разделяющими переменными можно руководствоваться следующим алгоритмом:

1) разделить переменные (с учетом условий, когда это можно делать);

2) интегрируя почленно полученные уравнения с разделенными переменными, найти его общий интеграл;

3) выяснить, имеет ли уравнение решения, не получающиеся из общего интеграла;

4) найти частный интеграл (или решение), удовлетворяющий начальным условиям (если это требуется).

Пример. Найти частное решение уравнения 2yy' = 1-3x² если y_o = 3 при x _o =1

Это уравнение с разделенными переменными. Представим его в дифференциалах:

dy

2y = 1- 3x²

dx

Отсюда 2y * dy = (1-3 x² ) dx

Интегрируем обе части последнего равенства, найдем ∫ 2y * dy = ∫ (1-3x²) dx получаем у² = x – x³ + C. Подставив начальные значения y_o = 3 x _o =1 найдем

С : 9 = 1-1+С т.е. С = 9.

Следовательно, искомый частный интеграл будет y² = x – x³ + 9 или

x³ + y² – x – 9 = 0

Тема 1.4. Ряды.

Определение 1. Числовым рядом называется выражение вида

а₁ + а₂ + …а_n + ………., где а₁, а₂, ……а_n – числа, принадлежащие некоторой определенной числовой системе.

Для сокращенного обозначения рядов используется знак суммирования Σ , а

_∞

именно а₁ + а₂ + …а_n + ……….= Σ a_n

^{n = 1}

Определение 2. Числа а₁,а_2, …а_n, …..называются членами ряда; а_n – называется общим членом ряда.

Определение 3. Ряд называется сходящимся, если последовательность его частных сумм S₁, S₂, S₃.........S_n, ...... сходится, т.е. если существует конечный предел

Lim S_n = S

^h→∞

Число S называется суммой ряда. Если Lim S_n не существует или Lim S_n = ∞, то ряд

^{h→∞ h→∞}

называется расходящимся и ему не приписывается никакое числовое значение.

Теорема 1. Если ряд сходится, то его общий член а_n стремится к нулю.

Если Lim а_n ≠ 0 или этот предел не существует, то ряд расходится.

^h→∞

Теорема 2. Пусть дан ряд а₁ + а₂ + …а_n + ……….,с положительными членами.

а_{n + 1} а_{n + 1}

Допустим, что Lim существует и Lim = Р

^h→∞ а_n ^h→∞ а_n

Тогда:

1) если Р<1, то ряд сходится

2) если Р>1, то ряд расходится.

Определение 3. Ряды, содержащие как положительные, так и отрицательные члены, называются закономерными.

Определение 4. Закономерный ряд называется абсолютно сходящимся, если сходится ряд

|а₁ | + |а₂ | + …+ | а_n | + ………., составленный из модулей его членов.

Определение 5. Ряд а₁ + а₂ + …а_n + ………., называется условно сходящимся, если он сходится, а ряд |а₁ | + |а₂ | + …+ | а_n | + ………., составленный из модулей его членов, расходится.

Определение 6. Ряд называется знакочередующимся, если положительные и отрицательные члены следуют друг за другом поочередно (а₁ + а₂ + а₃ – а₄ +…..+(-1)ⁿ⁺¹ *

*a_n + ....)

Теорема 3. Знакочередующимся ряд сходится, если:

1) его члены убывают по модулю,

а₁≥ а₂ ≥ … ≥а_n ≥ _……..

2) его общий член стремится к нулю,

lim а_n = 0

^h→∞

При этом сумма S ряда удовлетворяет неравенством 0≤ S ≤a₁

Определение 7. Пусть u₁ (x), u₂ (x),.....u_n (x) ... - некоторая последовательность функций.

_∞

Выражение вида Σ u_n(x) = u₁ (x), u₂ (x),.....u_n (x) + называется функциональным рядом.

ⁿ⁼¹

Определение 8. Функциональный ряд называется сходящимся в точке x_o , если

_∞

числовой ряд Σ u_n(x_o) = u₁ (x_o), u₂ (x_o),.....u_n (x_o) + ......

ⁿ⁼¹

полученный из функционального ряда подстановкой x = x_o , является сходящимся рядом. При этом называется точкой сходимости ряда.

Определение 9. Степенным рядом называется функциональный ряд вида

_∞

Σ a_n(x-x_o)ⁿ = a_o + a₁ (x-x_o), a₂ (x-x_o)²,.....a_n (x-x_o)ⁿ + ......

ⁿ⁼¹

где х – независимая переменная, х_o - фиксированное число, а_o, а₁, а₂, … а _n….. – постоянные коэффициенты.

Раздел 2.1. Основы дискретной математики.

Тема 2.1. Множества и отношения. Свойства отношений. Операции над множествами.

Множество – основное понятие а теории множеств, которое вводится без определения. О множестве известно как минимум то, что оно состоит из элементов.

Множество А называется

В

подмножеством множества В и обозна-

чается А Î В, если всякий элемент из А

А

является элементом В (рис.1)

рисунок 1

Способы задания множеств:

1. Перечислением, т.е. списком своих элементов.

2. Порождающей процедурой, которая описывает способ получения элементов множества из уже полученных элементов либо других объектов. В таком случае элементами множества являются все объекты, которые могут быть построены с помощью такой процедуры.

3. Описанием характеристических свойств, которыми должны обладать его элементы.

Пример 1

Задать различными способами множество N всех натуральных чисел 1, 2, 3…..

а) списком множество N задать нельзя ввиду его бесконечности.

б) порождающая процедура содержит два правила:

1) 1 Î N ; 2) если n Î N, то n + 1 Î N

в) описание характеристического свойства элементов множества N:

N = {х; х – целое положительное число}

Операции над множествами.

1. 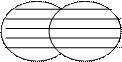Объединением множеств А и В называется

множество состоящее из всех тех элементов,

которые принадлежат хотя бы одному из множеств

А, В. (рисунок 2)

Рисунок 2

2. Пересечением множеств А и В называется

множество, состоящее из всех тех и только тех элементов,

которые принадлежат и А и В. ( рисунок 3)

Рисунок 3

3. Разностью множеств А и В называется множество

всех тех и только тех элементов А, которые

не содержатся в В. (рис.4)

Рисунок 4

4. Дополнением (до В) множества А называется В

А

множество всех элементов, не принадлежащих А (рис.5)

Рисунок 5

Пример 2

Осуществить операции над множествами А= {a, b, c, d} и B = {c,d,f.g,h}

A U B ={a, b, c, d, e, f.g,h}

A ∩ B = {c, d}

Операции дополнения над множествами А и В не могут быть выполнены т.е. универсальное множество не определено.

Отношения – один из способов задания взаимосвязей между элементами множества. Наиболее изученными и чаще всего используемыми являются так называемые упарные и бипарные отношения.

Отношения можно задать:

- списком;

- матрицей.

Свойства отношений.

Пусть R - отношение на множестве М, R ≤ М х М, тогда:

1. R – рефлексивно, если имеет место а R а для любого а Î М.

2. R – антирефлексивно, если ни для каждого а Î М не выполняется а R а.

3. R – симметрично, если а R b влечет bRа.

4. R – антисемметрично, если aRb и bRa влекут a=b, т.е. ни для каких различающихся элементов a и b (a≠b) не выполняется одновременно aRb и bRa .

5. R– транзитивно, если aRb и bRa влекут aRc.

Тема 2.2 Основные понятия теории графов

Графические представления в широком смысле – любые наглядные отображения исследуемой системы, процесса, явления на плоскости. К ним могут быть отнесены рисунки, чертежи, графики зависимостей характеристик, план-карты местностей, блок-схемы процессов, диаграммы и т.п.

Графические представления – удобный способ иллюстрации содержания различных понятий, относящихся к другим способам формализованных представлений.

Мощным и наиболее исследованным классом объектов, относящихся к графическим представлениям, являются так называемые графы.

Теория графов имеет огромные приложения, так как ее язык, с одной стороны, нагляден и понятен, а с другой – удобен в формальном исследовании.

Графические представления в узком смысле – это описание исследуемой системы, процесса, явления средствами теории графов в виде совокупности двух классов объектов: вершин и соединяющих их линий – ребер или дуг.

Определение: графом Д называется совокупность двух множеств: вершин V и ребер E, между элементами которых определено отношение инцидентности – каждое ребро е Е инцидентно равно двум вершинам v', v'' V, которые оно соединяет.

Так же о теории графов, об элементах графов, ознакомится с видами графов и рассмотреть операции над ними, вы можете изучая раздел 3 «Теория графов», стр.195-214 в учебнике для ХХ1 века под редакцией Г.И.Москинова «Дискретная математика».

Для самостоятельного изучения темы 3.1. Основы теории вероятностей и математической статистики. Вероятность. Теоремы сложения и умножения вероятностей. Темы 3.2. Случайная величина, ее функция распределения. Темы 3.3. Математическое ожидание и дисперсия случайной величины. Можно использовать следующую литературу: В.С.Щипачева «Основы высшей математики», а так же И.П.Натансон. Краткий курс высшей математики или Н.В.Богомолов Практическое занятие по математике.