Формирование сигналов амплитудной модуляции
Как известно, амплитудно-модулированный сигнал описывается выражением:
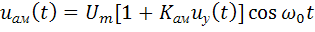 , (2.12)
, (2.12)
где 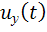 – управляющий (модулирующий) сигнал;
– управляющий (модулирующий) сигнал; 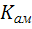 – коэффициент амплитудной модуляции;
– коэффициент амплитудной модуляции; 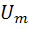 и
и 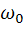 – соответственно, амплитуда и частота несущего колебания.
– соответственно, амплитуда и частота несущего колебания.
Представив (2.12) в виде:
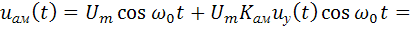
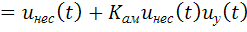 , (2.13)
, (2.13)
нетрудно убедится в том, что амплитудно-модулированное колебание является результатом добавления к сигналу несущего колебания произведения управляющего сигнала 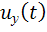 и сигнала несущей. Таким образом, при построении амплитудных модуляторов основной задачей является реализация перемножения двух сигналов: управляющего сигнала и сигнала несущего колебания.
и сигнала несущей. Таким образом, при построении амплитудных модуляторов основной задачей является реализация перемножения двух сигналов: управляющего сигнала и сигнала несущего колебания.
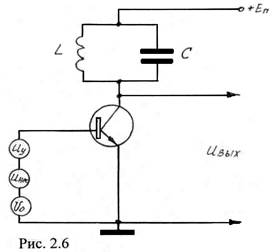 Эта задача решается с помощью нелинейного усилителя (Рис. 2.6), нагрузкой которого является колебательный контур, настроенный на частоту несущего колебания, и на вход которого поступает сигнал:
Эта задача решается с помощью нелинейного усилителя (Рис. 2.6), нагрузкой которого является колебательный контур, настроенный на частоту несущего колебания, и на вход которого поступает сигнал:
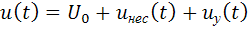 . (2.14)
. (2.14)
Выбором напряжения смещения 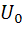 , обеспечим режим без отсечки тока (степенную аппроксимацию ВАХ транзистора):
, обеспечим режим без отсечки тока (степенную аппроксимацию ВАХ транзистора):
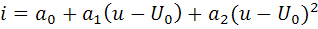 . (2.15)
. (2.15)
Подстановка (2.14) в (2.15) дает:
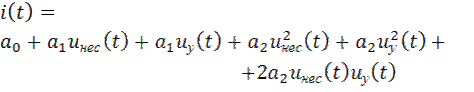 . (2.16)
. (2.16)
Разделив обе части (2.16) на 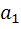 получим:
получим:
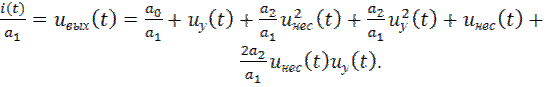 (2.17)
(2.17)
Последние два слагаемых в (2.17) представляют собой в соответствии с (2.13) амплитудно-модулированный сигнал с коэффициентом 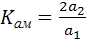 , который выделяется на нагрузке усилителя:
, который выделяется на нагрузке усилителя:
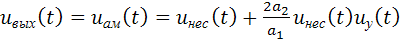 (2.18)
(2.18)
При однотональной амплитудной модуляции:
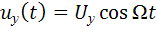 .
.
Подстановка этого выражения в (2.18) после элементарных преобразований дает:
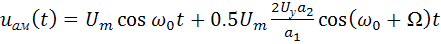 ,
,
где 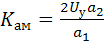 – коэффициент амплитудной модуляции.
– коэффициент амплитудной модуляции.
Режим без отсечки тока (степенная аппроксимация ВАХ) позволяет обеспечить 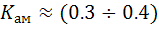 .
.
Для обеспечения больших значений 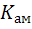 используют режим с отсечкой тока при аппроксимации:
используют режим с отсечкой тока при аппроксимации:
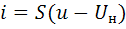 , при
, при 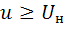 . (2.19)
. (2.19)
Подстановка (2.14) в (2.19) после преобразований дает:
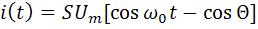 ,
,
где 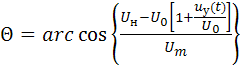 – угол отсечки, изменяющийся в соответствии с изменением
– угол отсечки, изменяющийся в соответствии с изменением 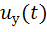 .
.
Амплитуда первой гармоники тока:
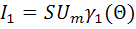 , (2.20)
, (2.20)
также будет изменяться в соответствии с изменением 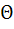 , а следовательно и
, а следовательно и 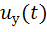 .
.
Амплитуда напряжения на выходе усилителя:
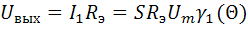 .
.
Важнейшей характеристикой модулятора является его модуляционная характеристика, т.е. зависимость амплитуды первой гармоники коллекторного тока транзистора от амплитуды 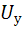 управляющего сигнала, т.е.
управляющего сигнала, т.е. 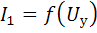 . Эта характеристика должна быть линейной в диапазоне изменений
. Эта характеристика должна быть линейной в диапазоне изменений 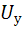 от минимального до максимального значений. Так как амплитуда первой гармоники зависит от угла отсечки как функция Берга [выражение (2.20)], то зависимость
от минимального до максимального значений. Так как амплитуда первой гармоники зависит от угла отсечки как функция Берга [выражение (2.20)], то зависимость 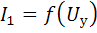 будет линейной в пределах линейного участка
будет линейной в пределах линейного участка 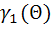 . Анализ графика зависимости
. Анализ графика зависимости 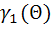 (см. рекомендованную литературу) показывает, что эта зависимость имеет линейный характер в пределах
(см. рекомендованную литературу) показывает, что эта зависимость имеет линейный характер в пределах 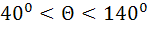 . При этом функция Берга изменяется от
. При этом функция Берга изменяется от 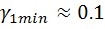 до
до 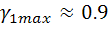 . Зная эти значения можно определить максимальное значение
. Зная эти значения можно определить максимальное значение 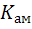 :
:
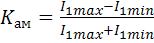 ,
,
или подставляя в это выражения формулу (2.20):
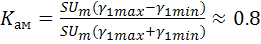 .
.
