Особенности решения системы линейных однородных уравнений

Однородным называется уравнение, у которого свободный член равен нулю.

Система линейных однородных уравнений всегда совместна, т.к. обладает нулевым решением.

Если в системе линейных однородных уравнений число независимых уравнений меньше числа неизвестных ( 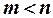), то она неопределенная, т.к. помимо нулевого решения обладает бесконечным множеством ненулевых решений.

Вопросы для самопроверки

¨ Что включает в себя множество, называемое векторным пространством, и какие операции в нем определены?

Какой размерности векторное пространство составляют решения совместной системы линейных уравнений с 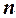неизвестными?

Что представляет собой сумма векторов?

Что представляет собой произведение вектора на число?

Какой вектор называется линейной комбинацией других векторов?

Чем различаются линейно зависимые и линейно независимые системы векторов?

Выполнение какой зависимости свидетельствует о линейной зависимости векторов?

Что называется базисом векторного пространства?

Какая система единичных векторов служит базисом 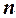-мерного векторного пространства?

Сколько различных линейно независимых систем векторов существует в векторном пространстве?

Из скольких векторов состоит каждый базис 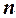-мерного векторного пространства?

Как называется максимальное число линейно независимых строк или столбцов матрицы?

Какое число называется минором 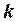-ого порядка матрицы ?

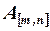О какой зависимости между строками или столбцами квадратной матрицы свидетельствует равенство нулю ее определителя?

Если в определенной матрице минор некоторого порядка равен нулю, то чему равны миноры более высокого порядка в этой же матрице?

Как получается окаймляющий минор?

Что можно сказать о решении системы 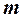линейных уравнений с 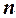неизвестными, если ранг матрицы ее коэффициентов при неизвестных равен рангу соответствующей расширенной матрицы?

Что можно сказать о решении системы 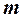линейных уравнений с 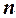неизвестными, если ранг матрицы ее коэффициентов при неизвестных меньше ранга соответствующей расширенной матрицы?

Что можно сказать о решении системы 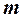линейных уравнений с 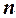неизвестными, если ранг матрицы ее коэффициентов при неизвестных равен рангу соответствующей расширенной матрицы и равен числу, меньшему числа неизвестных?

Что можно сказать о решении системы 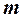линейных уравнений с 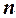неизвестными, если ранг матрицы ее коэффициентов при неизвестных равен рангу соответствующей расширенной матрицы и равен числу неизвестных, не большему числа уравнений?

Сколько переменных системы линейных уравнений можно назвать базисными, а сколько – свободными, если ранг матрицы этой системы равен числу уравнений, меньшему числа неизвестных?

Чем определяется максимально возможное число групп базисных переменных?

Какие уравнения называются однородными?

В каком случае система линейных однородных уравнений является неопределенной?