Краткие теоретические сведения. Для стальной балки, схема которой изображена в таблице 6.1, задана нагрузка и длина отрезка l

Задача 6

РАСЧЁТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ БАЛКИ

Условие задачи

Для стальной балки, схема которой изображена в таблице 6.1, задана нагрузка и длина отрезка l. Исходные значения приведены в таблице 6.2.

требуется подобрать номер двутаврового поперечного сечения.

Краткие теоретические сведения

Заданная балка имеет более трёх опорных усилий, поэтому она статически неопределима, и в ней невозможно найти значения опорных усилий, используя только уравнения статики. Для расчёта такой балки нужно составить столько дополнительных уравнений, сколько дополнительных опорных связей было установлено. Как известно, число, равное количеству дополнительных связей, называют степенью статической неопределимости С.

На рис. 6.1, а изображён общий вид статически неопределимой балки (его назовём регулярный вид или регулярная схема). Эта балка имеет крайние и промежуточные опоры. Одна из крайних опор балки всегда неподвижна, а все остальные опоры горизонтально подвижны. Расстояние между опорами называют пролётами балки. Опоры между крайними опорами называют промежуточными, их количество равно степени статической неопределимости.

По общему виду статически неопределимой балки видно, что её можно представить как непрерывный ряд двухопорных балок, жёстко соединённых торцами над промежуточными опорами. Отсюда понятно название, которое закрепилось за такой балкой: её называют неразрезной балкой.

Известно, что при раскрытии неопределимости можно брать разные варианты основной системы, но стремятся выбрать более эффективную.

Если основную систему для неразрезной балки выбирать отбрасыванием промежуточных опор, чтобы за лишние неизвестные взять реактивные силы промежуточных опор, то уже при с 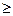2 математические вычисления громоздки. Для неразрезной балки предложена другая основная система – это разрезание балки над промежуточными опорами: пролеты разрезают, лишив их моментной связи друг с другом, что позволяет получить последовательность определимых двухопорных балок, связанных между собой горизонтальной связью. Говорят, что «вставляем» шарниры над промежуточными опорами (рис. 6.1, б). В этом варианте основной системы в качестве неизвестных опорных связей («лишних» связей) выступают изгибающие моменты над промежуточными опорами: например, на трёх соседних опорах имеем 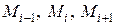(рис. 6.1, в).

а б в г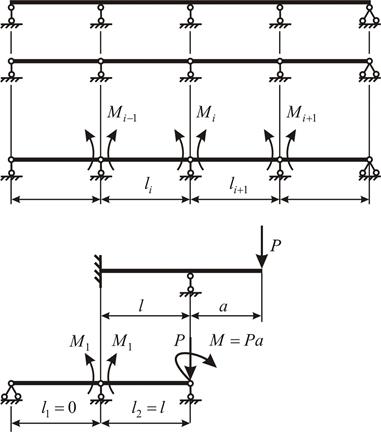

Рис. 6.1

Сечения балки над промежуточными опорами поворачиваются на определённый угол, но он для левого и правого пролётов одинаков по величине. Можно сказать, что разность углов поворота опорных сечений слева и справа над промежуточными опорами равна нулю, – в этом состоит физический смысл составления дополнительных уравнений (уравнений перемещений), которые после математической подстановки принимают вид уравнения трёх моментов. Для i-й опоры оно записывается так:

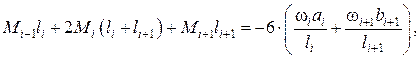(6.1)

где l_i, l_i+1 – длины соседних пролётов; ω_i, ω_i+1 – площади фигур изгибающих моментов от внешних нагрузок в этих пролётах; а_i – расстояние от центра тяжести площади ω_i до левой опоры; b_i+1 – расстояние от центра тяжести площади ω_i+1 до правой опоры.

При расчёте неразрезной балки составляем С таких уравнений (по числу степени статической неопределимости). Направление неизвестных моментов принимаем положительное: они растягивают нижние волокна (рис. 6.1, в). Если после вычисления моменты отрицательны, то это означает, что в действительности опорные моменты направлены в обратную сторону (т. е. растягивают верхние волокна). Нумерацию пролётов начинаем с крайнего левого, который обозначается цифрой 1, длина его – l₁; нумерация опор начинается с крайней левой, которая обозначается цифрой 0.

Если заданная балка имеет заделку или консоль, то её нужно привести к регулярной схеме балки (рис. 6.1, г): добавить со стороны заделки фиктивный пролёт длиной 0; консольную часть балки отбросить и перенести нагрузку консоли на крайнюю опору, добавив момент от переноса силы.

Определение опорных моментов по (6.1) составляет суть раскрытия статической неопределимости неразрезной балки. Далее можно выполнять требуемые расчёты на прочность и жёсткость.

Пример решения задачи 6

Для стальной балки (рис. 6.2, а) задана нагрузка: q = 18 кН/м, P = 0,6ql. Длина l = 4 м.