Краткие теоретические сведения. ТЕМА: Решение трансцендентных уравнений
ТЕМА: Решение трансцендентных уравнений
Содержание документа:
| 3.1 | Задание | 1 |
| 3.2 | Краткие теоретические сведения | 2 |
| 3.3 | Пример выполнения задания в среде Excel | 4 |
| 3.4 | Пример выполнения задания в среде Mathcad | 9 |
| 3.5 | Контрольные вопросы | 10 |
| 3.6 | Таблица индивидуальных вариантов | 11 |
Задание.
Изучить теоретический и вспомогательный материал, изложенный в лекции «Решение трансцендентных уравнений» и в данных методических указаниях.
Задача 1.Средствами Excel выполнить отделение корней трансцендентного уравнения F(x)=0 на промежутке [хн,хк]. Построить график функции F(x) на промежутке [хн,хк].
Задача 2.Средствами Excel по результатам выполнения задачи 1 найти корни уравнения методом дихотомий или методом хорд и методом простых итераций.
ВНИМАНИЕ. Студенты подгрупп СВ-111 и СВ-121 выполняют решение задачи методом дихотомий, а студенты подгрупп СВ-112 и СВ-122– методом хорд. Кроме этого все студенты выполняют решение задачи методом простых итераций.
Задача 3.Используя результаты отделения корней решить заданное уравнение средствами Mathcad. Построить график функции F(x).
Для защиты задания представить на компьютере Excel- и Mathcad-файлы решения задачи и рукописный отчет. В отчете представить:
1) запись исходного уравнения F(x)=0и промежутка [хн,хк] поиска корня в соответствии с вариантом;
2) результат отделения корней;
3) значение корня уравнения и количество итераций для его достижения для значений точности 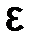 =0.0001, полученные в среде Excel методом дихотомий или методом хорд;
=0.0001, полученные в среде Excel методом дихотомий или методом хорд;
4) преобразование исходного уравнения к виду, необходимому для использования метода простых итераций и выполнения условия сходимости метода;
5) значение корня уравнения и количество итераций для его достижения для значений точности 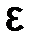 =0.0001, полученные в среде Excel методом простых итераций;
=0.0001, полученные в среде Excel методом простых итераций;
6) значение корня уравнения с точностью до 5 дробных разрядов, полученное в среде Matcad;
7) ответы на контрольные вопросы.
Краткие теоретические сведения
Существует несколько различных методов численного решения трансцендентных уравнений, но все они предполагают выполнение двух этапов: первый из них называется "отделение корней", второй - "уточнение корней".
На этапе отделения корней определяются те интервалы заданного промежутка [хнач, хкон], в каждом из которых расположен один и только один корень уравнения F(x)=0. Отделение корней можно выполнить с помощью следующих трех действий:
1) разбиение промежутка [хнач, хкон] на некоторое количество частей с шагом h,
2) вычисление функции F(x) в точках разбиения,
3) выбор таких промежутков разбиения, на концах которых функция F(x) принимает значения разных знаков.
На этапе уточнения корней постановка задачи выглядит так: найти корень уравнения F(x)=0, содержащийся внутри интервала (А,В) с заданной точностью ε. Предполагается, что границы интервала (А,В) найдены на этапе отделения корней.
При уточнении корней методом дихотомий каждое новое приближение Р определяется как середина интервала (А, В), т.е.
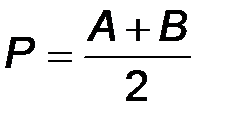 .
.
Для дальнейшего приближения выбирается та половина (А, В), на концах которой F(x) имеет разные знаки. Алгоритм выбора нужной половинки (А, Р) или (Р, В) изображен на блок-схеме:
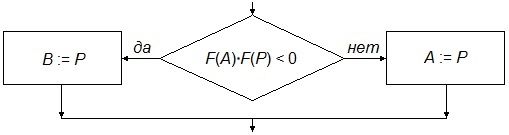
Если произведение значений F(А) и F(Р) отрицательное, то значит они имеют разные знаки, т.е. корень уравнения находится в половинке (А, Р) и, следовательно, точка B переносится в точку Р, в противном случае – в половинке (Р, В) и тогда точка А переносится в точку Р.
Критерием окончания итерационного процесса является выполнение неравенства
| В-А | < ε.
При уточнении корней методом хорд каждое новое приближение Р определяется как точка пересечения с осью ОХ прямой линии, соединяющей точки (А, F(A))и(B, F(В)), т.е.
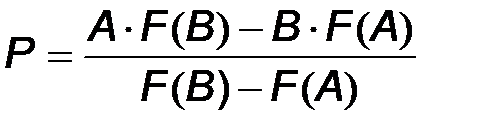 .
.
Как и в методе дихотомий, для дальнейшего приближения выбирается тот отрезок (А, Р), или (Р, В), на концах которого F(x) имеет разные знаки. В зависимости от этого точка А или точка В переносится в точку Р. Критерием окончания итерационного процесса является выполнение неравенства
|Pk - Pk-1|<ε,
где Pk-1, Pk -– два последовательных приближения к корню.
Для уточнения корней методом простых итерации необходимо исходное уравнение F(x)=0 преобразовать к эквивалентному уравнению x = φ(х). Тогда вычислительный процесс метода простых итераций выглядит так:
- выбираем начальное приближение x0 как любую точку интервала (А, В);
- вычисляем значение φ(х0) и называем его x1, т.е. x1 = φ(х0);
- вычисляем значение φ(х1) и называем его x2, т.е. x2 = φ(х1);
Повторяя эту процедуру, будем иметь в общем виде на некотором k-м шаге:
xk = φ (xk-1).
При выполнении условия сходимости 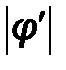 <1 последовательность х0,x1,x2,…xk, приближается к искомому корню.
<1 последовательность х0,x1,x2,…xk, приближается к искомому корню.
Критерием окончания вычислительного процесса является выполнение неравенства ½xk - xk-1½< ε.
Сходимость метода простых итераций обеспечивается должным выбором преобразования уравнения F(x)=0 к виду x = φ(х). Существует более или менее универсальный способ преобразования:
| F(x) = 0 | Þ | C . F(x) = 0 | Þ | C . F(x) + x = x | , |
т.е. φ(х) выбирается в виде φ(х) = C . F(x) + x, а константа С определяется из условия сходимости метода.
Рассмотрим в общем виде процесс определения константы С. Если функция φ(х)=C.F(x)+x, то условие сходимости метода простых итераций 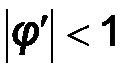 выглядит так:
выглядит так: 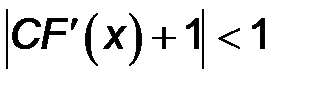 . Так как это неравенство содержит знак модуля, то оно распадается на два неравенства:
. Так как это неравенство содержит знак модуля, то оно распадается на два неравенства:
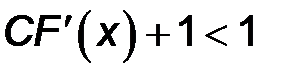 и и | 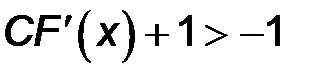 |
или
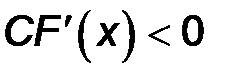 и и | 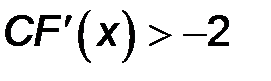 |
При 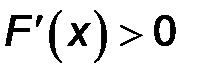 получаем
получаем 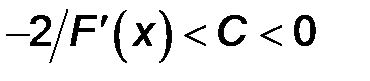 .
.
При 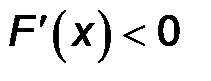 получаем
получаем 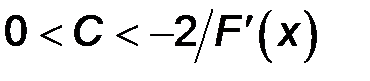 .
.
Окончательное значение С выбирается как середина найденного интервала 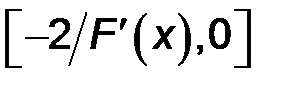 или
или 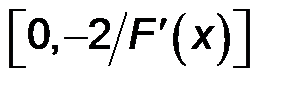 .
.
Более подробную информацию о методе простых итераций и вопросах его сходимости, а также о других методах численного решения трансцендентных уравнений можно найти в лекции «Решение трансцендентных уравнений».
