Метод анализа размерностей при изучении химико-технологических процессов

Теория подобия применяется при изучении сложных процессов и дает возможность получать уравнения подобия, описывающие эти процессы. Применять теорию подобия можно лишь тогда, когда удается составить дифференциальное уравнение, описывающее изучаемый процесс, и сформулировать условия однозначности.

Однако при изучении очень сложных процессов в ряде случаев не удается составить даже дифференциальное уравнение, описывающее процесс. В таких случаях для получения уравнения подобия применяют метод анализа размерностей.

Применение метода анализа размерностей возможно только в том случае, когда в результате предварительного опытного изучения процесса известно, какие параметры существенно влияют на течение этого процесса.

Так, при исследованиях течения жидкости по трубе найдено, что на перепад давления в трубе влияют диаметр d и длина l трубы, плотность ρ, вязкость μ и скорость ω протекающей жидкости, т. е.

Δp = f(d, I, ρ, μ, ω) (1)

Метод анализа размерностей позволяет из общей функциональной зависимости вида (1) получить уравнение подобия, описывающее изучаемый процесс. При этом обязательным является условие, чтобы единицы измерения всех величин, входящих в общую функциональную зависимость, были выражены в одной системе.

Количество чисел подобия, входящих в искомое уравнение подобия исследуемого процесса, можно найти по установленной общей функциональной зависимости с помощью π-теоремы, которая гласит: если общая функциональная зависимость связывает между собой п размерных величин, при составлении которых использовано m первичных единиц измерения, то эта функциональная зависимость может быть представлена в виде уравнения подобия, содержащего п—m чисел подобия, составленных из величин, входящих в общую функциональную зависимость.

В приведенном примере в уравнение (1) входят шесть величин (n = 6), имеющих в системе СИ следующие размерности:

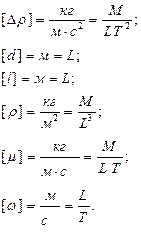
При составлении размерностей этих шести величин использованы три первичные единицы измерения (m=3): м, с, кг. На основании π-теоремы уравнение (1) может быть представлено в виде уравнения подобия, в которое входит п—т = 6—3 = 3 числа подобия.

Это легче всего показать на примере. Представим общую функциональную зависимость (1) в виде произведения входящих в нее величин в некоторых степенях:

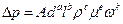(2)

Величины, входящие в уравнение (2), заменим формулами размерностей этих величин:

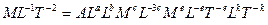
или

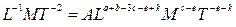(3)

Далее, приравнивая показатели степеней при одинаковых символах размерностей, получим три уравнения с пятью неизвестными:

a+b-3c-e+k=-1 (а); c+e=1 (б); -e-k=-2 (в).

Поскольку эта система уравнений не может быть решена, так как в ней не хватает двух уравнений, выразим все неизвестные величины через какие-нибудь две, например через е и b:

из (б) с = 1 — е; из (в) k = 2 — е;

из (а) а = —b — е,

Полученные значения а, с и k подставим в уравнение (2):

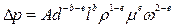
Сгруппируем величины по показателям степеней:

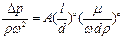(4)

Уравнение (4) представляет собой уравнение подобия, описывающее течение жидкости по трубе. В это уравнение входят три числа подобия, которые называют числами гидродинамического подобия:

число Эйлера 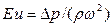(5)

число Рейнольдса 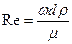(6)

параметрическое число (критерий) геометрического подобия

Г = l/d. (7)

Эти числа подобия применяют при рассмотрении различных процессов в последующих главах курса.

Постоянные А, b, е в уравнении (4) определяют на основании опытных данных.

Следует отметить, что при применении метода анализа размерностей не удается сформулировать условия однозначности, а, следовательно, разделить числа подобия на определяющие и неопределяющие. Кроме того, вследствие недостаточного предварительного изучения процесса из анализа могут выпасть некоторые величины, существенно влияющие на течение процесса, а также включены для анализа величины, не влияющие на процесс.

Основы гидрокинетики

В химических и нефтехимических производствах многие процессы приводят к образованию неоднородных смесей, которые в дальнейшем подлежат разделению. Часто встречаются и задачи противоположного характера: из веществ, находящихся в различных агрегатных состояниях, необходимо получить смесь. Решения как первой, так и второй задачи основываются на гидрокинетических закономерностях осаждения и фильтрования.

Гидрокинетикой в дальнейшем будем называть часть гидродинамики, которая составляет теоретические основы для определения кинетических закономерностей процессов осаждения и фильтрования.