Постановка и математическая модель транспортной задачи

Начнём с постановки транспортной задачи и её математической модели.

Имеется сеть поставщиков P₁, P₂, …, P_m некоторого однородного груза, и сеть потребителей П₁, П₂, …, П_n этого груза. Известны: запасы поставщиков a₁, a₂, …, a_m, соответственно; потребности потребителей b₁, b₂, …, b_n, соответственно; стоимость c_ij перевозки единицы груза от i-го поставщика к j-му потребителю. Требуется составить такой план перевозок (то есть определить, кто, кому и в каком количестве должен отгрузить груз), чтобы запасы поставщиков были полностью использованы, потребности потребителей полностью были удовлетворены, и суммарная стоимость перевозок была минимальной.

Условия задачи обычно даются в следующей транспортной таблице:

bj ai	b1	b2	…	bj	…	bn
a1	c11	c12	…	c1j	…	c1n
…	…	…	…	…	…	…
ai	ci1	ci2	…	cij	…	cin
…	…	…	…	…	…	…
am	cm1	cm2	…	cmj	…	cmn

К клетке, стоящей на пересечении строки a_i и столбца b_j, будем ссылаться как к клетке (i, j).

Пример 1.

			Таблица 8.1
bj ai

В таблице имеем m=3, n=4, a₁=90, a₂=30, a₃=40 - запасы поставщиков, b₁=70, b₂=30, b₃=20, b₄=40 - потребности потребителей. Также, например, c₁₂=3 означает, что перевозка единицы груза от первого поставщика ко второму потребителю обходится в 3 условные единицы, а, например, c₃₃=4 означает, что перевозка единицы груза от третьего поставщика к третьему потребителю обходится в 4 условные единицы.

Составим математическую модель задачи.

Пусть x_ij - количество груза, перевозимого от i-го поставщика к j-му потребителю. Так как c_ij - стоимость перевозки единицы груза от i-го поставщика к j-му потребителю, то перевозки от i-го поставщика к j-му потребителю обойдутся в c_ijx_ij условных единиц, а в сумме перевозки обойдутся в c₁₁x₁₁+c₁₂x₁₂+…= 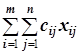условных единиц. Таким образом, 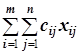- целевая функция, которую необходимо минимизировать (суммарная стоимость перевозок должна быть минимальной): 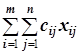® min.

Далее, 1-й поставщик отгружает потребителям x₁₁+x₁₂+…+x_1n единиц груза, и он должен отгрузить все свои запасы: x₁₁+x₁₂+…+x_1n=a₁. И, вообще, рассуждая относительно i-го поставщика, получаем уравнение x_i1+x_i2+…+x_in=a_i (i=1, 2, …, m).

Аналогично рассуждая по j-му потребителю (j=1, 2, …, n), получаем уравнения x_1j+x_2j+…+x_mj=b_j (j=1, 2, …, n).

Наконец, количество x_ij перевозимого груза не может быть отрицательным: x_ij³0.

Таким образом, математическая модель транспортной задачи - следующая:

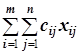® min

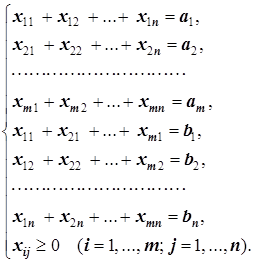(8.1)

Как видим, задача (8.1) - это задача линейного программирования. Поэтому на неё распространяются все понятия общей задачи линейного программирования: базис, опорное решение и т.д. В частности, к ней можно применить теорию двойственности. Наконец, к ней можно применить симплекс-метод. Тем не менее, задача имеет свою специфику, заключающуюся в первую очередь в том, что её матрица ограничений состоит из 0 и 1, причём в каждом столбце имеется в точности по две 1. Поэтому естественно ожидать, что для её решения применим метод, более эффективный, чем симплекс-метод. Таким методом является метод потенциалов. Прежде, чем привести алгоритм этого метода, приведём некоторые необходимые теоретические сведения.