Спектр последовательности прямоугольных импульсов

Вернемся к рассмотренному выше примеру с системой связи и рассмотрим спектр периодической последовательности прямоугольных импульсов s_r(t) (рис. 2.5) с периодом Т₀, амплитудой А и длительностью Т.

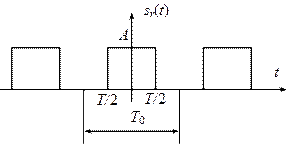
Рис. 2.5 Последовательность импульсов

Коэффициенты ряда Фурье для такого сигнала:

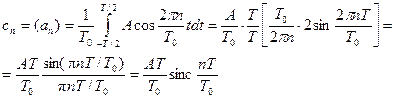(33)

В данном выражении

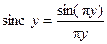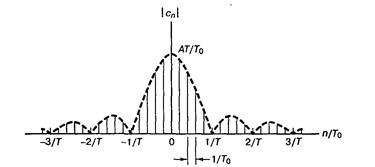
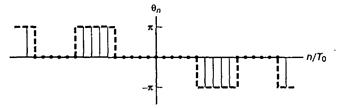
функция sinc, как показано на рис. 2.6, достигает максимума (единицы) при у = 0и стремится к нулю при у ® ±¥, осциллируя с постепенно уменьшающейся амплитудой. Через нуль она проходит в точках у = ±1, ±2, …. На рис. 2.7, а как функция отношения п/Т₀показан амплитудный спектр последовательности импульсов |с_n|, а на рис. 2.7, б изображен фазовый спектр q_n. Следует отметить, что положительные и отрицательные частоты двустороннего спектра — это полезный способ математического выражения спектра; очевидно, что в реальных условиях воспроизвести можно только положительные частоты.

Отношение

q = T0/T

(34)

называют скважностью импульсов. Обратное отношение носит название коэффициента заполнения.

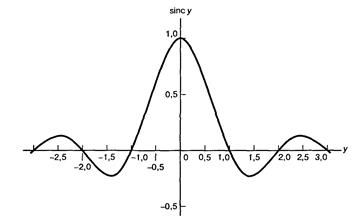
Рис. 2.6. Функция sinc

а)

б)

Рис. 2.7. Спектр последовательности импульсов:

а) амплитудный; б) фазовый

Синтез выполняется посредством подстановки коэффициентов из формулы (33) в формулу (10). Получаемый ряд представляет исходную последовательность импульсов s_r(t), синтезированную из составных элементов.

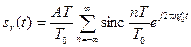c

(25)

Идеальная периодическая последовательность импульсов включает все гармоники, кратные собственной частоте. В системах связи часто предполагается, что значительная часть мощности или энергии узкополосного сигнала приходится на частоты от нуля до первого нуля амплитудного спектра (рис. 2.7, а). Таким образом, в качестве меры ширины полосы последовательности импульсов часто используется величина 1/T (где Т — длительность импульса). Отметим, что ширина полосы обратно пропорциональна длительности импульса; чем короче импульсы, тем более широкая полоса с ними связана. Отметим также, что расстояние между спектральными линиями Df= 1/Т₀обратно пропорционально периоду импульсов; при увеличении периода линии располагаются ближе друг к другу.

Таблица 2.1. Фурье-образы

x(t)	X(f)
d(t)
	d(f)
cos 2pf0t	[d(f - f0) + d(f + f0)]/2
sin 2pf0t	[d(f - f0) - d(f + f0)]/2
d(t - t0)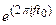
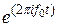	d(f - f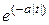0)
, a>0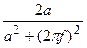
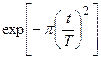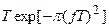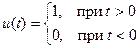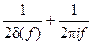exp(-at)u(t), a>0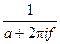
rect(t / T)	T sinc fT
W sinc Wt	rect (f / W)

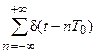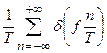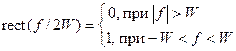sinc x =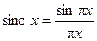

Таблица 2.2 Свойства преобразования Фурье

Действие	x(t)	X(f)
Изменение масштаба	x(at)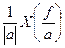
Сдвиг по времени	x(t - t0)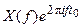
Сдвиг по частоте		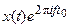X(f - f0)
Дифференцирование по времени		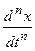(-2pif)nX(f)
Дифференцирование по частоте	(-2pit)nx(t)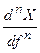
Интегрирование по времени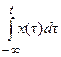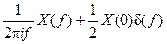
Свертка по времени	x1(t) * x2(t)	X1(f)X2(f)
Свертка по частоте	x1(t)x2(t)	X1(f)*X2(f)