Тема: Линейные отображения
ДЕ1.Абстрактная алгебра
1)Тема: Группы и подгруппы
Группу по сложению образует множество …
 | целых чисел |
| натуральных чисел | |
| натуральных чисел с нулем | |
| действительных чисел без нуля |
Тема: Дробно-рациональные функции
Разложение дробно-рациональной функции  на простые дроби над полем вещественных чисел имеет вид …
на простые дроби над полем вещественных чисел имеет вид … 
Решение: 
Получаем систему трех уравнений с тремя неизвестными: 
Тогда 
3)Тема: Основные алгебраические структуры
В кольце квадратных матриц второго порядка единичный элемент … – это матрица

Тема: Линейные отображения
Пусть  базис пространства
базис пространства  Операторы
Операторы  и
и  этого пространства заданы матрицами
этого пространства заданы матрицами 
 . Тогда матрица оператора
. Тогда матрица оператора  равна
равна 
Решение: 
Тема: Дробно-рациональные функции
Разложение дробно-рациональной функции  на простые дроби над полем вещественных чисел имеет вид …
на простые дроби над полем вещественных чисел имеет вид … 
Тема: Линейные отображения
Линейный оператор  отображает базис
отображает базис  в векторы:
в векторы: 

 Тогда матрица оператора
Тогда матрица оператора  в этом базисе имеет вид …
в этом базисе имеет вид … 
Решение:

Тема: Основные алгебраические структуры
В кольце целых четных чисел единичный элемент …
 | не существует |
Решение:
В кольце целых четных чисел единичный элемент не существует.
Тема: Группы и подгруппы
Группу по умножению образует множество …
 | действительных чисел без нуля |
| действительных чисел | |
| целых чисел | |
| натуральных чисел с нулем |
Решение:
Группу образует множество действительных чисел без нуля с введенной операцией умножения чисел. Все остальные множества групп не образуют, так как, например, нуль не имеет обратного элемента.
Тема: Группы и подгруппы
Операция «+» – сложения образует группу на множестве …
 | целых четных чисел |
| натуральных чисел | |
| целых нечетных чисел | |
| действительных чисел без нуля |
Решение:
Множество целых четных чисел с введенной операцией сложения образует группу. Множество натуральных чисел не группа, так как, например, 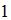 не имеет противоположного элемента. Множество целых нечетных не имеет нулевого элемента, как и множество действительных чисел без нуля.
не имеет противоположного элемента. Множество целых нечетных не имеет нулевого элемента, как и множество действительных чисел без нуля.
Тема: Линейные отображения
Из заданных операторов пространства  – пространства трехмерных векторов, линейным является оператор …
– пространства трехмерных векторов, линейным является оператор … 
Тема: Основные алгебраические структуры
В кольце целых четных чисел единичный элемент …
 | не существует |
равен 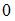 | |
равен 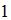 | |
равен 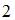 |
Решение:
В кольце целых четных чисел единичный элемент не существует.
Тема: Основные алгебраические структуры
Подалгеброй алгебры  является совокупность …
является совокупность …
 |  |
 | |
 | |
 |
Решение:
Совокупности  и
и  не являются подалгебрами алгебры
не являются подалгебрами алгебры  , так как,
, так как,  .
.
Совокупность  не является подалгеброй алгебры
не является подалгеброй алгебры  , так как множество
, так как множество  не замкнуто относительно умножения.
не замкнуто относительно умножения.
Совокупность  является подалгеброй алгебры
является подалгеброй алгебры  , так как
, так как  и множество
и множество  замкнуто относительно умножения.
замкнуто относительно умножения.
Тема: Группы и подгруппы
Подгруппой группы целых чисел с введенной операцией сложения является множество …
 | четных целых чисел |
| нечетных целых чисел | |
| натуральных чисел | |
| натуральных чисел с нулем |
Тема: Дробно-рациональные функции
Множество всех дробно-рациональных функций образует поле 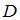 относительно обычных операций сложения и умножения таких функций.
относительно обычных операций сложения и умножения таких функций.
Пусть  и
и  , причем
, причем  и
и 
Тогда числитель произведения  равен …
равен …
 | |
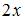 | |
 | |
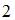 |
Решение:
Разложим на линейные множители знаменатели дробно-рациональных функций  и
и  :
:


Тогда  .
.
То есть числитель произведения  равен 1.
равен 1.
Тема: Дробно-рациональные функции
Разложение дробно-рациональной функции  на элементарные дроби имеет вид …
на элементарные дроби имеет вид …
 |  |
 | |
 | |
 |
Решение:
Выполним деление заданных полиномов «уголком»:

Разложим знаменатель на простые множители:  .
.
Тогда

Тема: Группы и подгруппы
Группу по умножению образует множество …
 | действительных чисел без нуля |
| действительных чисел | |
| целых чисел | |
| натуральных чисел с нулем |
Решение:
Группу образует множество действительных чисел без нуля с введенной операцией умножения чисел. Все остальные множества групп не образуют, так как, например, нуль не имеет обратного элемента.
Тема: Линейные отображения
Из заданных операторов пространства  – пространства трехмерных векторов, линейным является оператор …
– пространства трехмерных векторов, линейным является оператор …
 |  |
 | |
 | |
 |
Решение:
Линейным называется отображение 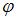 удовлетворяющее условиям:
удовлетворяющее условиям:
 ,
,
 .
.
Проверим на линейность оператор  :
:
 ,
,
 ,
,
Следовательно  - первое условие не выполнено, а значит
- первое условие не выполнено, а значит  не является линейным оператором.
не является линейным оператором.
Для оператора  проверим выполнение второго условия:
проверим выполнение второго условия:

Условие не выполняется, значит  не линейный оператор.
не линейный оператор.
Проверим выполнение второго условия для оператора  :
:

Следовательно, данный оператор не является линейным.
Проверим выполнение условий линейности для оператора  :
:
 ,
,
 ,
,
Следовательно  – первое условие выполнено.
– первое условие выполнено.
 – второе условие выполнено. Поэтому
– второе условие выполнено. Поэтому  является линейным оператором.
является линейным оператором.
Тема: Основные алгебраические структуры
Подалгеброй алгебры  является совокупность …
является совокупность …
 |  |
 | |
 | |
 |
Решение:
Подалгеброй алгебры  , называют совокупность
, называют совокупность  , где
, где  , причем
, причем  замкнуто относительно всех операций из
замкнуто относительно всех операций из 
 не является подалгеброй алгебры
не является подалгеброй алгебры  , так как
, так как 
 и
и  не являются подалгебрами алгебры
не являются подалгебрами алгебры  , так как, не совпадают множества заданных операций.
, так как, не совпадают множества заданных операций.
 является подалгеброй алгебры
является подалгеброй алгебры  , так как
, так как  и каждая главная операция является ограничением соответствующей операции на
и каждая главная операция является ограничением соответствующей операции на 
Тема: Основные алгебраические структуры
 является подалгеброй алгебры …
является подалгеброй алгебры …
 |  |
 | |
 | |
 |
Решение:
 является подалгеброй алгебры
является подалгеброй алгебры  , так как
, так как  и каждая главная операция является ограничением соответствующей операции на
и каждая главная операция является ограничением соответствующей операции на  .
.
Тема: Дробно-рациональные функции
Разложение дробно-рациональной функции  на элементарные дроби имеет вид
на элементарные дроби имеет вид 
Тема: Линейные отображения
Образом вектора  при линейном преобразовании, заданном матрицей
при линейном преобразовании, заданном матрицей  , является вектор …
, является вектор …
 |  |
 | |
 | |
 |
Решение:
Так как образ  вектора
вектора  определяется по формуле:
определяется по формуле:  , то
, то  .
.
Тема: Основные алгебраические структуры
Подалгеброй алгебры  является совокупность …
является совокупность …
 |  |
 | |
 | |
 |
Решение:
Подалгеброй алгебры  , называют совокупность
, называют совокупность  , где
, где  , причем
, причем  замкнуто относительно всех операций из
замкнуто относительно всех операций из 
 не является подалгеброй алгебры
не является подалгеброй алгебры  , так как
, так как 
 и
и  не являются подалгебрами алгебры
не являются подалгебрами алгебры  , так как, не совпадают множества заданных операций.
, так как, не совпадают множества заданных операций.
 является подалгеброй алгебры
является подалгеброй алгебры  , так как
, так как  и каждая главная операция является ограничением соответствующей операции на
и каждая главная операция является ограничением соответствующей операции на 
Тема: Группы и подгруппы
Мультипликативная группа рациональных чисел – это множество рациональных чисел …
 | без нуля с операцией умножения |
| с операцией сложения | |
| с операцией умножения | |
| без нуля с отношением порядка |
Решение:
Мультипликативная группа определяется операцией умножения.
Поэтому множество рациональных чисел с операцией сложения и множество рациональных чисел без нуля с отношением порядка не являются мультипликативными группами.
Множество рациональных чисел с операцией умножения не является группой, так как для элемента 0 нет обратного относительно умножения.
Тогда мультипликативная группа рациональных чисел – это множество рациональных чисел без нуля с операцией умножения.
Тема: Дробно-рациональные функции
Множество всех дробно-рациональных функций образует поле 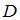 относительно обычных операций сложения и умножения таких функций.
относительно обычных операций сложения и умножения таких функций.
Пусть  и
и  , причем
, причем  и
и 
Тогда числитель суммы  равен …
равен …
 |  |
 | |
 | |
 |
Решение:
Разложим на линейные множители знаменатели дробно-рациональных функций  и
и  :
:


Тогда

То есть, числитель суммы  равен
равен  .
.
Тема: Линейные отображения
Линейное преобразование  в базисе
в базисе  имеет матрицу
имеет матрицу  . Тогда матрица этого оператора в базисе
. Тогда матрица этого оператора в базисе  , где
, где  ;
;  , имеет вид …
, имеет вид …
 |  |
 | |
 | |
 |
Решение:
Матрица оператора  в базисе
в базисе  вычисляется по формуле
вычисляется по формуле  , где
, где 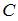 – матрица перехода от базиса
– матрица перехода от базиса  к базису
к базису  .
.
Матрица перехода  , тогда
, тогда  . Матрица линейного оператора
. Матрица линейного оператора  . Тогда
. Тогда  .
.
Тема: Группы и подгруппы
Коммутативной группой является множество …
 | квадратных матриц с введенной операцией сложения |
| невырожденных квадратных матриц с введенной операцией умножения | |
| натуральных чисел с 0, с введенной операцией сложения | |
| натуральных чисел с введенной операцией сложения |
Решение:
Множество квадратных матриц с введенной операцией сложения образует группу: ассоциативность выполняется, нейтральным элементом группы является нулевая матрица, для любой матрицы существует противоположная.
Множество невырожденных квадратных матриц с введенной операцией умножения образует группу, но она не является коммутативной, т.к. не для любых матриц 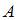 и
и  выполняется равенство
выполняется равенство  .
.
Множество натуральных чисел (с 0, или без него) с введенной операцией сложения не является группой, т.к. нет противоположного элемента, например, у элемента 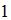 .
.
Тема: Основные алгебраические структуры
Для кольца  множество
множество  , рассматриваемое с одной алгебраической операцией сложения, представляет собой …
, рассматриваемое с одной алгебраической операцией сложения, представляет собой …
 | абелеву группу |
| поле | |
| целостное кольцо | |
| область целостности |
Решение:
Для кольца  множество
множество  , рассматриваемое с одной алгебраической операцией сложения, представляет собой абелеву группу.
, рассматриваемое с одной алгебраической операцией сложения, представляет собой абелеву группу.
Тема: Линейные отображения
Дано линейное преобразование векторов на плоскости  , которое каждый вектор переводит в вектор той же длины, но противоположно направленный исходному. Тогда матрица
, которое каждый вектор переводит в вектор той же длины, но противоположно направленный исходному. Тогда матрица 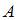 этого преобразования имеет вид …
этого преобразования имеет вид …
 |  |
 | |
 | |
 |
Решение:
Так как  и
и  , то матрица такого линейного преобразования имеет вид
, то матрица такого линейного преобразования имеет вид  .
.
Тема: Основные алгебраические структуры
В кольце квадратных матриц второго порядка единичный элемент …
 | – это матрица  |
– это матрица  | |
– это матрица  | |
| не существует |
Тема: Дробно-рациональные функции
Даны два полинома:  и
и 
Тогда целая часть от деления полинома  на полином
на полином  равна …
равна …
 |  |
 | |
 | |
 |
Решение:
Выполним деление заданных полиномов «уголком»:

Тогда:

То есть, целая часть от деления полинома  на полином
на полином  равна
равна 
ема: Основные алгебраические структуры
Элемент  называется обратным к элементу
называется обратным к элементу 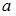 в группе G с единичным элементом
в группе G с единичным элементом  , если …
, если …
 |  |
 , ,  | |
 | |
 |
Тема: Группы и подгруппы
Подгруппой группы целых чисел с введенной операцией сложения является множество …
 | четных целых чисел |
| нечетных целых чисел | |
| натуральных чисел | |
| натуральных чисел с нулем |
Решение:
Данное подмножество должно быть замкнуто относительно операций сложения и взятия противоположного элемента. Этим условиям удовлетворяет, например, множество четных целых чисел.
Тема: Линейные отображения
Линейным отображением пространства трехмерных векторов на пространство двумерных векторов является …
 |  |
 | |
 | |
 |
Решение:
Линейным называется отображение 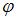 удовлетворяющее условиям:
удовлетворяющее условиям:
 ,
,
 .
.
Проверим на линейность отображение  :
:
 ,
,
 ,
,
Следовательно  – первое условие не выполнено, а значит
– первое условие не выполнено, а значит  не является линейным отображением.
не является линейным отображением.
Для отображения  проверим выполнение второго условия:
проверим выполнение второго условия:

Условие не выполняется, значит  не линейное отображение.
не линейное отображение.
Проверим выполнение второго условия для отображения  :
:

Следовательно, данное отображение не является линейным.
Проверим выполнение условий линейности для отображения  :
:
 ,
,
 ,
,
Следовательно  – первое условие выполнено.
– первое условие выполнено.
 – второе условие выполнено. Поэтому
– второе условие выполнено. Поэтому  является линейным отображением.
является линейным отображением.
