Экономический смысл теории двойственности
Данную задачу можно интерпретировать с экономической точки зрения.
Согласно следствию к третьей теореме двойственности, при увеличении ресурса 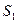 на одну единицу, оптимальное значение прибыли при реализации готовой продукции возрастет на
на одну единицу, оптимальное значение прибыли при реализации готовой продукции возрастет на 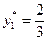 д.е; при увеличении ресурса
д.е; при увеличении ресурса 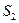 на одну единицу, оптимальное значение прибыли возрастет на
на одну единицу, оптимальное значение прибыли возрастет на 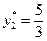 д.е. Увеличение же не дефицитных ресурсов не увеличит прибыль, это видно из того, что
д.е. Увеличение же не дефицитных ресурсов не увеличит прибыль, это видно из того, что 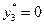 ,
, 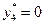 . То есть компоненты оптимального решения двойственной задачи, являются оценками степени дефицитности имеющихся ресурсов для производства запланированной продукции и могут служить мерой дефицитности ресурсов. Дефицитный ресурс (полностью используемый по оптимальному плану производства) имеет положительную оценку, а ресурс избыточный (используемый не полностью) имеет нулевую оценку
. То есть компоненты оптимального решения двойственной задачи, являются оценками степени дефицитности имеющихся ресурсов для производства запланированной продукции и могут служить мерой дефицитности ресурсов. Дефицитный ресурс (полностью используемый по оптимальному плану производства) имеет положительную оценку, а ресурс избыточный (используемый не полностью) имеет нулевую оценку
Теперь предположим, что существует некоторая организация желающая выкупить ресурсы 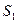 ,
, 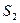 ,
, 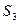 ,
, 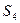 , имеющиеся в наличии у предприятия. Естественно, организация хотела бы выкупить у предприятия ресурсы, неся при этом как можно меньшие денежные затраты. Поэтому перед администрацией предприятия возникает новая задача: найти оптимальные оценки
, имеющиеся в наличии у предприятия. Естественно, организация хотела бы выкупить у предприятия ресурсы, неся при этом как можно меньшие денежные затраты. Поэтому перед администрацией предприятия возникает новая задача: найти оптимальные оценки 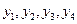 на единицу каждого вида ресурса
на единицу каждого вида ресурса 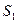 ,
, 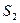 ,
, 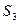 ,
, 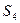 соответственно, такие, что продажа ресурсов по этим оценкам была бы не менее выгодна, чем продажа готовой продукции, которую могло бы произвести предприятие из имеющихся ресурсов.
соответственно, такие, что продажа ресурсов по этим оценкам была бы не менее выгодна, чем продажа готовой продукции, которую могло бы произвести предприятие из имеющихся ресурсов.
В качестве оценки единицы ресурса каждого вида, возьмем оценки оптимального решения двойственной задачи, т.е. оценим ресурсы в зависимости от степени их дефицитности для организации производства продукции 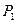 и
и 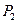 . В этом случае
. В этом случае
1) 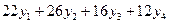 д.е. – стоимостная оценка всех имеющихся ресурсов, которая с учетом интересов покупающей организации минимизируется;
д.е. – стоимостная оценка всех имеющихся ресурсов, которая с учетом интересов покупающей организации минимизируется;
2) 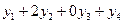 д.е. – стоимостная оценка на прибыль, получаемую при продаже ресурсов необходимых для производства одной единицы продукции
д.е. – стоимостная оценка на прибыль, получаемую при продаже ресурсов необходимых для производства одной единицы продукции 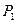 , которая в соответствии с интересами продающего ресурсы предприятия должна быть не меньше, чем прибыль (4 д.е.), получаемая при реализации единицы готовой продукции
, которая в соответствии с интересами продающего ресурсы предприятия должна быть не меньше, чем прибыль (4 д.е.), получаемая при реализации единицы готовой продукции 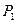 .
.
3) 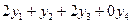 д.е. – стоимостная оценка на прибыль, получаемую при продаже ресурсов необходимых для производства одной единицы продукции
д.е. – стоимостная оценка на прибыль, получаемую при продаже ресурсов необходимых для производства одной единицы продукции 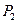 , должна быть не меньше 3 д.е.
, должна быть не меньше 3 д.е.
Учитывая то, что стоимостные оценки 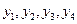 не могут быть отрицательными, строим модель задачи, получим модель (4.6).
не могут быть отрицательными, строим модель задачи, получим модель (4.6).
Задачи для самостоятельного решения
Задача №4.2.
Составить и решить задачу двойственную задаче:
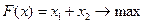 при условии выполнения ограничений
при условии выполнения ограничений
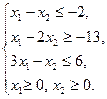
Задача №4.3.
Используя графический метод и теоремы двойственности найти минимум целевой функции 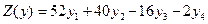 при условии выполнения ограничений:
при условии выполнения ограничений:
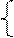
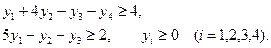
Задача №4.4
Используя графический метод и теоремы двойственности найти максимум целевой функции 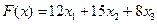 при условии выполнения ограничений:
при условии выполнения ограничений:
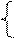
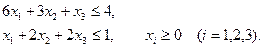
Задача №4.5.
Построить и решить с использованием теории двойственности задачу двойственную задаче №2.6.
Задача №4.6.
Построить и решить с использованием теории двойственности задачу двойственную задаче №1.2. Воспользоваться решением задачи № 2.10.
Задача №4.7.
Построить и решить с использованием теории двойственности задачу двойственную задаче №1.11. Воспользоваться решением задачи № 2.11.
Задача №4.8.
Построить и решить с использованием теории двойственности задачу двойственную задаче №1.19. Воспользоваться решением задачи № 2.12.
Транспортная задача
Транспортная задача – это задача о минимизации транспортных расходов, связанных с обеспечением пунктов потребления определенным количеством однородной продукции (груза), производимой (хранимой) в нескольких пунктах производства (хранения).
В общем виде задача может быть сформулирована следующим образом. Однородный груз, сосредоточенный в  пунктах
пунктах 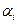 производства (хранения), необходимо распределить между
производства (хранения), необходимо распределить между  пунктами
пунктами 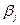 потребления. Стоимость перевозки единицы груза известна для всех маршрутов. Необходимо составить такой план перевозок, при котором выполнялись бы следующие условия:
потребления. Стоимость перевозки единицы груза известна для всех маршрутов. Необходимо составить такой план перевозок, при котором выполнялись бы следующие условия:
1) запросы всех пунктов потребления должны быть удовлетворены;
2) имеющиеся мощности поставщиков реализованы;
3) общие транспортные расходы по доставке груза были бы минимальными.
Примем следующие обозначения:
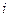 - - | номер пункта производства (хранения) (i=1,2,…,m); |
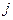 - - | номер пункта потребления (j=1,2,…,n); |
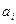 - - | количество груза, имеющегося в i-ом пункте производства (мощность поставщика); |
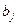 - - | количество груза, необходимое для j-го пункта потребления; |
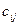 - - | стоимость перевозки единицы груза из i-го пункта отправления в j-ый пункт назначения (коэффициенты затрат); |
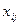 - - | количество груза, планируемого к перевозке от i-го пункта отправления в j-ый пункт назначения. |
Исходные данные описанной задачи удобно записать в таблицу, которую называют распределительной таблицей транспортной задачи.
| Поставщи- ки | потребители | Запасы | ||||
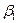 | … | 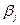 | … | 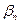 | ||
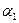 | 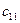 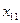 | … | 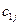 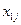 | … | 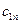 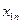 | 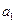 |
| … | … | … | … | … | … | … |
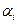 | 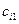 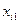 | … | 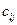 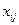 | … | 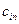 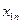 | 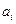 |
| … | … | … | … | … | … | … |
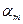 | 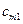 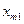 | … | 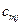 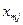 | … | 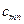 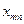 | 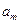 |
| Потребности | 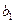 | … | 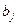 | … | 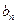 |
