Понятие о функциональной и корреляционной связи

Тема «Статистическое изучение взаимосвязей между явлениями»

Понятие о функциональной и корреляционной связи

Корреляционно-регрессионный анализ

Регрессионный анализ

Понятие о функциональной и корреляционной связи

Между общественными и экономическими явлениями имеется два основных типа связи ¾ функциональная и статистическая (называемая также стохастической, вероятностной или корреляционной). Перед тем как рассмотреть их подробнее, введем понятия независимых и зависимых признаков.

Независимыми,или факторными, называют признаки, которые вызывают изменения других, связанных с ними признаков. Признаки, изменение которых под воздействием определенных факторов требуется проследить, называют зависимыми, или результативными.

При функциональной связиизменение независимых переменных приводит к получению точно определенных значений зависимой переменной.

Наиболее часто функциональные связи проявляются в естественных науках, например в механике функциональной является зависимость расстояния, пройденного объектом, от скорости его движения и т. п.

Пристатистической связикаждому значению независимой переменной Х соответствует множество значений зависимой переменной Y, причем не известно заранее, какое именно. Например, мы знаем, что прибыль коммерческого банка определенным образом связана с размером его уставного капитала (этот факт не подлежит сомнению). Тем не менее, нельзя вычислить точную величину прибыли при заданном значении последнего показателя, так как она зависит еще и от множества других факторов, помимо размера уставного капитала, среди которых имеются и случайные. В нашем случае, скорее всего, мы определим лишь среднее значение прибыли, которое будет получено в целом по совокупности банков со сходным объемом уставного капитала. Таким образом, статистическая связь отличается от функциональной наличием действия на зависимую переменную большого числа факторов.

Заметим, что статистическая связь проявляется лишь «в общем и среднем» при большом числе наблюдений за явлением. Так, интуитивно мы можем предполагать, что существует зависимость между объемом основных фондов предприятия и получаемой им прибылью, а именно с увеличением первого размер прибыли возрастает. Но на это можно возразить и привести пример предприятия, обладающего достаточным количеством современного производственного оборудования, но тем не менее терпящего убытки. В данном случае мы имеем наглядный пример статистической связи, которая проявляется лишь в больших совокупностях, содержащих десятки и сотни единиц в отличие от функциональной, подтверждающейся для каждого наблюдения.

Корреляционнойявляется статистическая связь между признаками, при которой изменение значений независимой переменной Х приводит к закономерному изменению математического ожидания случайной величины Y.

Пример 1.Предположим, что имеются данные по предприятиям о размере нераспределенной прибыли предыдущего года, объеме инвестиций в основной капитал и о суммах, выделенных на приобретение ценных бумаг (тыс. ден. ед.):

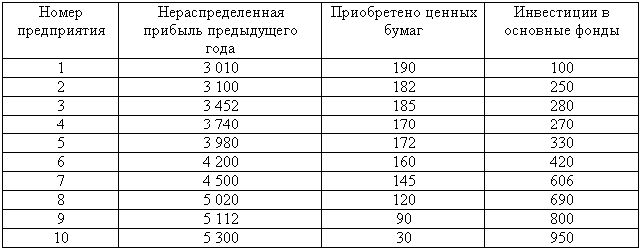
Из таблицы видно, что имеется прямое соответствие между нераспределенной прибылью предприятия и его инвестициями в основной капитал: при увеличении нераспределенной прибыли объем инвестиций также возрастает. Теперь обратим внимание на связь между показателем нераспределенной прибыли и объемом приобретенных ценных бумаг. Здесь она носит совершенно иной характер: увеличение первого показателя приводит к прямо противоположному эффекту ¾ стоимость приобретенных ценных бумаг за редким исключением (что уже однозначно исключает наличие функциональной связи) уменьшается. Такой визуальный анализ данных, при котором наблюдения ранжируются по возрастанию или убыванию независимой величины х, а затем анализируется изменение значений зависимой величины у, называется методом приведения параллельных данных.

В рассмотренном примере в первом случае связь прямая, т. е. увеличение (уменьшение) одного показателя влечет увеличение (уменьшение) другого (наблюдается соответствие в изменениях показателей), а во втором ¾ обратная, т. е. уменьшение одного показателя вызывает рост другого или же увеличение одного соответствует снижению другого.

Прямая и обратная зависимости характеризуют направление связи между признаками, которую можно проиллюстрировать графически с помощью поля корреляции. При его построении в прямоугольной системе координат на оси абсцисс располагают значения независимой переменной х, а на оси ординат ¾ зависимой у. Пересечение координат обозначают точками, которые символизируют наблюдения. По форме рассеяния точек на корреляционном поле судят о форме и тесноте связи. На рисунке 1 приводятся корреляционные поля, соответствующие различным формам связи.

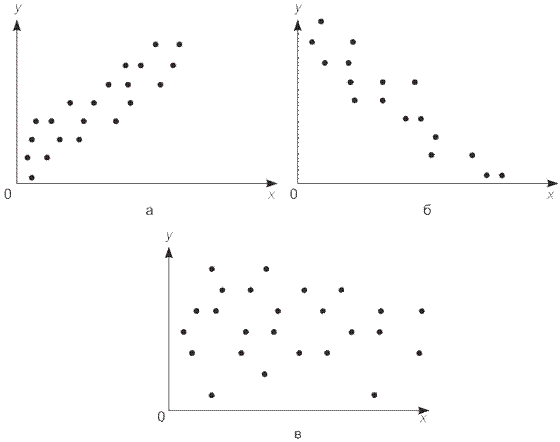
Рис. 1. Корреляционные поля: а ¾ прямая (положительная) связь; б ¾ обратная (отрицательная) связь; в ¾ отсутствие связи

Раздел статистической науки, занимающийся исследованием причинных связей между социально-экономическими явлениями и процессами, имеющими количественное выражение,¾ это корреляционно-регрессионный анализ. По существу имеются два отдельных направления анализа ¾ корреляционный и регрессионный. Однако в связи с тем, что на практике они применяются чаще всего комплексно (исходя из результатов корреляционного анализа проводят регрессионный), их объединяют в один вид.

Проведение корреляционно-регрессионного анализа предполагает решение следующих задач:

1) выявление из большого числа факторов наиболее информативных, оказывающих более существенное воздействие на результативную величину (предварительный анализ, базирующийся на простейших методах выявления зависимостей и экспертных оценках);

2) определение направления и количественной оценки тесноты зависимости между факторной величиной Х и результативной Y (при этом факторных переменных может быть достаточно много, тогда определяется множественная корреляция);

3) нахождение математической функции, описывающей зависимость результативного показателя Yот наиболее информативных факторных Х. Эта функция выполняет роль модели, которая аналитически выражает зависимость условного среднего значения результативного признака от факторных переменных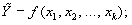

4) оценка качества полученной модели, определение возможной величины ошибки получаемых по этой модели прогнозных значений Y;

5) построение прогнозов.

Из перечисленных задач первые две относят непосредственно к задачам корреляционного анализа, три последующие ¾ к регрессионному анализу и только по отношению к количественным показателям.